Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T02:43:16.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Characters of Depth-Zero, Supercuspidal Representations of the Rank-2 Symplectic Group

Published online by Cambridge University Press:  20 November 2018

Clifton Cunningham
Clifton Cunningham*
Affiliation:
Department of Mathematics, University of Massachusetts, Amherst MA 01003-4515, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper expresses the character of certain depth-zero supercuspidal representations of the rank-2 symplectic group as the Fourier transform of a finite linear combination of regular elliptic orbital integrals—an expression which is ideally suited for the study of the stability of those characters. Building on work of F. Murnaghan, our proof involves Lusztig’s Generalised Springer Correspondence in a fundamental way, and also makes use of some results on elliptic orbital integrals proved elsewhere by the author using Moy-Prasad filtrations of 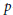$p$-adic Lie algebras. Two applications of the main result are considered toward the end of the paper.

Keywords

22E5022E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 306 - 331
Copyright
Copyright © Canadian Mathematical Society 2000

References

[AD] Adler, J. and Debacker, S., Moy-Prasad filtrations and harmonic analysis. Draft, 1997.Google Scholar
[Cu] Cunningham, C., Some results on elliptic orbital integrals. In preparation.Google Scholar
[K] Kazhdan, D., Proof of Springer's hypothesis. Israel J. Math. 28(1977), 272–286.Google Scholar
[KL] Kazhdan, D. and Lusztig, G., Fixed point varieties on affine flag manifolds. Israel J. Math. (2) 62(1988), 129–168.Google Scholar
[L.1] Lusztig, G., Intersection cohomology complexes on a reductive group. Invent.Math. 75(1984), 205–272.Google Scholar
[L.2] Lusztig, G., Character sheaves I. Adv. Math. 56(1985), 193–297.Google Scholar
Character sheaves II. Adv. Math. 57(1985), 226–265.Google Scholar
Character sheaves III. Adv. Math. 57(1985), 266–315.Google Scholar
Character sheaves IV. Adv. Math. 59(1986), 1–63.Google Scholar
Character sheaves V. Adv. Math. 61(1986), 103–155.Google Scholar
[Mu] Murnaghan, F., Characters of supercuspidal representations of classical groups. Ann. Sci. École Norm Sup. (4), (1) 29(1996), 45–105.Google Scholar
[MP] Moy, A. and Prasad, G., Jacquet functors and unrefined minimal K-types. Comment. Math. Helv. (1) 71(1996), 98–121.Google Scholar
[Sp] Spaltenstein, N., Polynomials over local fields, nilpotent orbits and conjugacy classes in Weyl groups. Astérisque 168(1988), 191–217.Google Scholar
[Wa.1] Waldspurger, J.-L., Quelques questions sur les intégrales orbitales unipotentes et les algèbres de Hecke. Bull. Soc. Math. France 124(1996), 1–34.Google Scholar
[Wa.2] Waldspurger, J.-L., Le lemme fondamental implique le transfert. Compositio Math. 105(1997), 153–236.Google Scholar