We formulate and prove a “winding number” index theorem for certain “Toeplitz” operators in the same spirit as Gohberg–Krein, Lesch and others. The “number” is replaced by a self-adjoint operator in a subalgebra 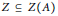$Z\,\subseteq \,Z\left( A \right)$ of a unital 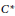$C*$-algebra, 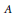$A$. We assume a faithful 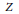$Z$-valued trace $\tau $ on 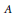$A$ left invariant under an action 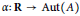$\alpha :\,\text{R}\,\to \,\text{Aut}\left( A \right)$ leaving 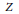$Z$ pointwise fixed. If 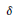$\delta $ is the infinitesimal generator of 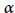$\alpha $ and 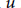$u$ is invertible in 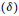$\text{dom}\left( \delta \right)$, then the “winding operator” of 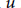$u$ is 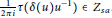$\frac{1}{2\pi i}\tau \left( \delta \left( u \right){{u}^{-1}} \right)\,\in \,{{Z}_{sa}}$. By a careful choice of representations we extend 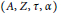$\left( A,\,Z,\,\tau ,\,\alpha \right)$ to a von Neumann setting 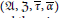$\left( \mathfrak{A},\,\mathfrak{Z},\,\bar{\tau },\,\bar{\alpha } \right)$ where 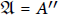$\mathfrak{A}\,=\,{A}''$ and 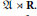$\mathfrak{Z}\,=\,{Z}''$. Then 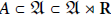$A\,\subset \,\mathfrak{A}\,\subset \,\mathfrak{A}\,\rtimes \,\mathbf{R}$, the von Neumann crossed product, and there is a faithful, dual 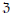$\mathfrak{Z}$-trace on 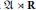$\mathfrak{A}\,\rtimes \,\mathbf{R}$. If 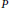$P$ is the projection in 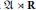$\mathfrak{A}\,\rtimes \,\mathbf{R}$ corresponding to the non-negative spectrum of the generator of 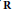$\mathbf{R}$ inside 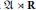$\mathfrak{A}\,\rtimes \,\mathbf{R}$ and 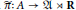$\tilde{\pi }:\,A\,\to \,\mathfrak{A}\,\rtimes \,\mathbf{R}$ is the embedding, then we define 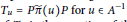${{T}_{u}}\,=\,P\tilde{\pi }\left( u \right)P\,\text{for}\,u\,\in \,{{A}^{-1}}$ and show it is Fredholm in an appropriate sense and the $\mathfrak{Z}$-valued index of 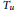${{T}_{u}}$ is the negative of the winding operator. In outline the proof follows that of the scalar case done previously by the authors. The main difficulty is making sense of the constructions with the scalars replaced by 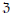$\mathfrak{Z}$ in the von Neumann setting. The construction of the dual 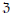$\mathfrak{Z}$-trace on 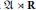$\mathfrak{A}\,\rtimes \,\mathbf{R}$ requires the nontrivial development of a 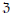$\mathfrak{Z}$-Hilbert algebra theory. We show that certain of these Fredholm operators fiber as a “section” of Fredholm operators with scalar-valued index and the centre-valued index fibers as a section of the scalar-valued indices.