Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:23:36.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Building a Stationary Stochastic Process From a Finite-Dimensional Marginal

Published online by Cambridge University Press:  20 November 2018

Marcus Pivato
Marcus Pivato*
Affiliation:
Department of Mathematics University of Toronto 100 St. George Street Toronto, Ontario M5S 3G3, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 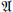$\mathfrak{A}$ is a finite alphabet, 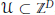$\mathcal{U}\,\subset \,{{\mathbb{Z}}^{D}}$, and 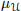${{\mu }_{\mathcal{U}}}$ is a probability measure on 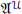${{\mathfrak{A}}^{\mathcal{U}}}$ that “looks like” the marginal projection of a stationary stochastic process on 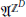${{\mathfrak{A}}^{{{\mathbb{Z}}^{D}}}}$, then can we “extend” 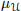${{\mu }_{\mathcal{U}}}$ to such a process? Under what conditions can we make this extension ergodic, (quasi)periodic, or (weakly) mixing? After surveying classical work on this problem when 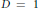$D\,=\,1$, we provide some sufficient conditions and some necessary conditions for 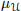${{\mu }_{\mathcal{U}}}$ to be extendible for 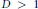$D\,>\,1$, and show that, in general, the problem is not formally decidable.

Keywords

37A5060G1037B10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 2 , 01 April 2001 , pp. 382 - 413
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] del Junco, Karin Reinhold Andres and Weiss, Benjamin, Partitions with independent iterates along IP sets. Ergodic Theory and Dynamical Systems (2) 19 (1999), 447–473.Google Scholar
[2] Berger, R., The undecidability of the domino problem. Mem. Amer.Math. Soc. 66(1966).Google Scholar
[3] Goles, Eric and Martinez, Servet, editors, Cellular Automata and Complex Systems. Kluwer Academic, Dordrecht, 1999.Google Scholar
[4] Furstenberg, H., Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, New Jersey, first edition, 1981.Google Scholar
[5] Gutowitz, Howard, editor, Cellular Automata: Theory and Experiment. Proceedings of an Interdisciplinary Workshop, Los Alamos, New Mexico, Amsterdam, 1989. Los Alamos, National Laboratory, North-Holland.Google Scholar
[6] Hedlund, G., Endomorphisms and automorphisms of the shift dynamical systems. Math. Systems Theory, 3 (1969), 320–375.Google Scholar
[7] Hopcroft, John E. and Ullman, Jeffrey D., Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Co., first edition, 1979.Google Scholar
[8] Katznelson, Yitzhak, An Introduction to Harmonic Analysis. Dover, New York, New York, USA, first edition, 1976.Google Scholar
[9] Kitchens, Bruce and Schmidt, K., Markov subgroups of (Z/2Z)Z2. In: Symbolic Dynamics and its Applications, (ed., Peter Walters), Contemporary Math. 135, Providence, 1992, 265–283.Google Scholar
[10] Kitchens, Bruce P., Symbolic dynamics: one-sided, two-sided, and countable state Markov shifts. Springer-Verlag, New York, 1998.Google Scholar
[11] Lind, Douglas and Marcus, Brian, An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, New York, first edition, 1995.Google Scholar
[12] Delorme, M. and Mazoyer, J., editors, Cellular Automata: A Parallel Model. Kluwer Academic, Dordrecht, 1999.Google Scholar
[13] Mozes, S.. Tilings, substitutions and the dynamical systems generated by them. J. AnalyseMath. 53 (1989), 139–186.Google Scholar
[14] Mozes, S., A zero entropy, mixing of all orders tiling system. In: Symbolic Dynamics and its Applications, (ed. Peter Walters), Contemporary Mathematics 135, Providence, 1992, 319–326.Google Scholar
[15] Markley, Nelson G. and Paul, Michael E., Maximal measures and entropy for Zν subshifts of finite type. In: Classical Mechanics and Dynamical Systems, (eds., R. Devaney and Z. Nitecki), Dekker Notes 70, 135–157.Google Scholar
[16] Markley, Nelson G. and Paul, Michael E., Matrix subshifts for Zν symbolic dynamics. Proc. LondonMath. Soc. (3) 43 (1981), 251–272.Google Scholar
[17] Parry, W., Intrinsic Markov chains. Trans. Amer.Math. Soc. 112 (1964), 55–66.Google Scholar
[18] Radin, C., Global order from local sources. Bull. Amer.Math. Soc. 25 (1991), 335–364.Google Scholar
[19] Robinson, Raphael M., Undecidability and nonperiodicity for tilings of the plane. Invent.Math. 12 (1971), 177–209.Google Scholar
[20] Rozanov, Yu. A., Markov Random Fields. Springer-Verlag, New York, first edition, 1982.Google Scholar
[21] Schlijper, A., On some variational approximations in two-dimensional classical lattice systems. PhD thesis, University of Groningen, The Netherlands, 1985.Google Scholar
[22] Smale, Stephen, Differentiable dynamical systems. Bull. Amer.Math. Soc. 73 (1967), 747–817.Google Scholar
[23] Farmer, Doyne, Toffoli, Tommaso and Wolfram, Stephen, editors, Cellular Automata. Proceedings of an Interdisciplinary Workshop, Los Alamos, New Mexico, Amsterdam, 1983, Los Alamos National Laboratory, North-Holland.Google Scholar
[24] Ulam, Stanislaw, Random processes and transformations. In: Sets, Numbers, and Universes, Cambridge, Massachusetts, MIT Press, 326–337.Google Scholar
[25] von Neumann, John, Theory of Self-Reproducing Automata. University of Illinois Press, Urbana, Illinois, 1966.Google Scholar
[26] Walters, Peter, An Introduction to Ergodic Theory. Springer-Verlag, New York, first edition, 1982.Google Scholar
[27] Wolfram, Stephen, Cellular Automata and Complexity. Addison-Wesley, Reading, Massachusetts, 1994.Google Scholar