Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T13:36:10.497Z Has data issue: false hasContentIssue false
  • English
  • Français

Brownian Motion and Dimension of Perfect Sets

Published online by Cambridge University Press:  20 November 2018

Robert Kaufman
Robert Kaufman*
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X(t) denote real-valued Brownian motion on the interval 0 ≦ t ≦ 1, so normalized that E(X2(t)) = t. We prove some theorems about transforms X(F) of closed sets F: in general, F is not known in advance but depends on X. The main point of comparison among sets is taken to be their Hausdorff dimension, and in this respect the linear process is quite different from the planar. We state and discuss briefly two theorems.

(A) It is almost sure that, for every closed set F in [0, 1],

(B) For each closed set F in (—00,00) and number a ,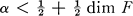

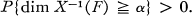
Plainly, statements (A) and (B) are nearly best possible. For the planar process dimX(F) = 2 dim F (with the same quantification as in (A)) [6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 674 - 680
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Kahane, J.-P., Propriétés locales des fonctions à séries de Fourier aléatoires, Studia Math. 19 (1960), 1–25.Google Scholar
2. Kahane, J.-P., Images browniennes des ensembles parfaits, C. R. Acad. Sci. Paris Sér. A-B 263 (1966), A613–A615.Google Scholar
3. Kahane, J.-P., Images d1 ensembles parfaits par des séries de Fourier gaussiennes, C. R. Acad. Sci. Paris Sér. A-B 263 (1966), A678–A681.Google Scholar
4. Kahane, J.-P. and Salem, R., Ensembles parfaits et séries trigonométriques, Actualités Sci. Indust., No. 1301 (Hermann, Paris, 1963).Google Scholar
5. Kaufman, R., On the zeroes of some random functions (to appear in Studia Math., 1970).Google Scholar
6. Kaufman, R., Une propriété métrique du mouvement brownien, C. R. Acad. Sci. Paris Sér. A-B 268 (1969), A727–A728.Google Scholar
7. Loève, M., Probability theory, 2nd éd., The University Series in Higher Mathematics (Van Nostrand, Princeton, N.J .-Toronto-New York-London, 1960).Google Scholar