No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
The Betti numbers βn(k) of the residue class field k = R/m of a commutative local ring (R, m) have been studied for about 20 years, primarily as the coefficients of the Poincaré series of E . Several authors have obtained results about the growth of the sequence {βn(k)}.For example, Gulliksen [3] showed that when R is non-regular, the sequence is non-decreasing. More recently, Avramov [1] studied asymptotic properties of {βn(k)} and found that under certain conditions the growth is exponential, i.e., there is a natural number p such that for all n, βpn(k) ≧ 2n.
In this paper, we examine the sequence {βn(M)} for arbitrary finitely generated non-free modules M over any commutative local artin ring R. We establish the following bounds:
1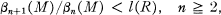
2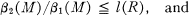
3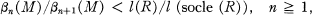
where l(X) is the length of X.