Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T13:41:23.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Structure of Hyperbolic 3-Manifolds Admitting Annular and Toroidal Fillings at Large Distance

Published online by Cambridge University Press:  20 November 2018

Sangyop Lee  and
Masakazu Teragaito
Sangyop Lee
Affiliation:
Department of Mathematical Sciences, Seoul National University, San 56-1, Shinrim-dong, Kwanak-gu, Seoul 151-747, Korea e-mail: [email protected]
Masakazu Teragaito
Affiliation:
Department of Mathematics and Mathematics Education, Hiroshima University, 1-1-1 Kagamiyama, Higashi-hiroshima, Japan 739-8524 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a hyperbolic 3-manifold 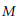$M$ with a torus boundary component, all but finitely many Dehn fillings yield hyperbolic 3-manifolds. In this paper, we will focus on the situation where 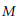$M$ has two exceptional Dehn fillings: an annular filling and a toroidal filling. For such a situation, Gordon gave an upper bound of 5 for the distance between such slopes. Furthermore, the distance 4 is realized only by two specific manifolds, and 5 is realized by a single manifold. These manifolds all have a union of two tori as their boundaries. Also, there is a manifold with three tori as its boundary which realizes the distance 3. We show that if the distance is 3 then the boundary of the manifold consists of at most three tori.

Keywords

57M50Secondary57N10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 164 - 188
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Culler, M., Gordon, C. M., Luecke, J., and Shalen, P., Dehn surgery on knots. Ann. of Math. 125(1987), no. 2, 237–300.Google Scholar
[2] Gordon, C. M., Boundary slopes on punctured tori in 3-manifolds. Trans. Amer. Math. Soc. 350(1998), 1713–1790.Google Scholar
[3] Gordon, C. M., Small surfaces and Dehn filling. In: Proceedings of the Kirbyfest, Geom. Topol. Monogr. 2, Geom. Topol. Publ., Coventry, 1999, pp. 177–199 (electronic).Google Scholar
[4] Gordon, C. M. and Luecke, J., Dehn surgeries on knots creating essential tori. I. Comm. Anal. Geom. 3(1995), no. 3-4, 597–644.Google Scholar
[5] Gordon, C. M. and Luecke, J., Toroidal and boundary-reducing Dehn fillings. Topology Appl. 93(1999), no. 1, 77–90.Google Scholar
[6] Gordon, C. M. and Wu, Y. Q., Toroidal and annular Dehn fillings. Proc. LondonMath. Soc. 78(1999), no. 3, 662–700.Google Scholar
[7] Gordon, C. M. and Wu, Y. Q., Annular and boundary reducing Dehn fillings. Topology 39(2000), no. 3, 531–548.Google Scholar
[8] Hayashi, C. and Motegi, K., Only single twists on unknots can produce composite knots. Trans. Amer. Math. Soc. 349(1997), no. 11, 4465–4479.Google Scholar
[9] Ichihara, K. and Teragaito, M., Klein bottle surgery and genera of knots. Pacific J. Math. 210 (2003), no. 2, 317–333.Google Scholar
[10] Jin, G., Lee, S., Oh, S., and Teragaito, M., P2-reducing and toroidal Dehn fillings. Math. Proc. Cambridge Philos. Soc. 134(2003), no. 2, 271–288.Google Scholar
[11] Lee, S., Oh, S., and Teragaito, M., Reducing Dehn fillings and small surfaces. Proc. London Math. Soc. 92(2006), no. 1, 203–223.Google Scholar
[12] Teragaito, M., Creating Klein bottles by surgery on knots. J. Knot Theory Ramifications 10(2001), no. 5, 781–794.Google Scholar
[13] Wu, Y. Q., Dehn fillings producing reducible manifolds and toroidal manifolds. Topology 37(1998), no. 1, 95–108.Google Scholar
[14] Wu, Y. Q., Sutured manifold hierarchies, essential laminations, and Dehn surgery. J. Differential Geom. 48(1998), no. 3, 407–437.Google Scholar