Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T16:37:57.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Bergman Spaces on Disconnected Domains

Published online by Cambridge University Press:  20 November 2018

Alexandru Aleman ,
Stefan Richter  and
William T. Ross
Alexandru Aleman
Affiliation:
Fachbereich Mathematik und Informatik, Fernuniversität Hagen, Postfach 940, 58084 Hagen, Germany, e-mail: Alexandru.Aleman@Fern Uni-Hagen.de
Stefan Richter
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, Tennessee, 37996-1300, U.S.A., e-mail: [email protected]
William T. Ross
Affiliation:
Department of Mathematics, University of Richmond, Richmond, Virginia 23173, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a bounded region G ⊂ ℂ and a compact set K ⊂ G, with area measure zero, we will characterize the invariant subspaces ℳ (under ƒ → zƒ) of the Bergman space 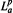(G \ K), 1 ≤ p < ∞, which contain 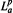(G) and with dim(ℳ/(z - λ)ℳ) = 1 for all λ ∈ G \ K. When G \ K is connected, we will see that dim(ℳ/(z - λ)ℳ) = 1 for all λ ∈ G \ K and thus in this case we will have a complete description of the invariant subspaces lying between 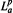(G) and 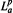(G \ K). When p = ∞, we will remark on the structure of the weak-star closed z-invariant subspaces between H∞(G) and H∞(G \ K). When G \ K is not connected, we will show that in general the invariant subspaces between 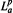(G) and 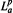(G \ K) are fantastically complicated. As an application of these results, we will remark on the complexity of the invariant subspaces (under ƒ → ζƒ) of certain Besov spaces on K. In particular, we shall see that in the harmonic Dirichlet space 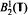, there are invariant subspaces ℱ such that the dimension of ζℱ in ℱ is infinite.

Keywords

47B3846E1546E35Bergman spacesinvariant subspacesdualitySobolev spacesBesov spacesHausdorff measurecapacity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 2 , 01 April 1996 , pp. 225 - 243
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Adams, R.A., Sobolev Spaces, New York, Academic Press, 1975.Google Scholar
2. Axler, S. and R Bourdon, Finite codimensional invariant subspaces of Bergman spaces, Trans. Amer. Math. Soc. 306 (1988), 805–817.Google Scholar
3. Bagby, T., Quasi topologies and rational approximation, J. Funct. Anal. 10 (1972), 259–268.Google Scholar
4. Banach, S.,Theorie des Opérations Linéaires, New York, Chelsea Publ. Co., 1955.Google Scholar
5. Bercovici, H., Foiaş, C. and Pearcy, C., Dual algebras with applications to invariant subspaces and dilation theory, CBMS Regional Conf. Ser. in Math. 56, Providence, Amer. Math. Soc, 1985.Google Scholar
6. Deny, J., Sur la convergence de certaines intégrates de la théorie du potentiel, Arch. Math. 5 (1954), 367–370.Google Scholar
7. Evans, L.C. and Gariepy, R.F.,Measure theory and fine properties of Junctions, Stud. Adv. Math., Boca Raton, Florida, CRC Press, 1991.Google Scholar
8. Havin, V.P., Approximation in the mean by analytic functions, Soviet Math. Dokl. 9 (1968), 245–248.Google Scholar
9. Hedberg, L .I., Non-linear potentials and approximation in the mean by analytic functions, Math. Z. 129 (1972), 299–319.Google Scholar
10. Hedenmalm, H., An invariant subspace of the Bergman space having the co-dimension two property, J. Reine Angew. Math. 443 (1993), 1–9.Google Scholar
11. Iwaniec, T., The best constant in a BMO-inequalityfor the Beurling-Ahlfors transform, Michigan Math. J. 33 (1986), 387–394.Google Scholar
12. Jonsson, A. and Wallin, H.,Function spaces on subsets of Rn, Math. Reports 2, London, Paris, Utrecht, New York, Harwood Academic Publishers, 1984.Google Scholar
13. Maz'ya, V.G. and Shaposhnikova, T.O., Theory of Multipliers in Spaces of Differentiable Functions, Boston, Pitman Press, 1985.Google Scholar
14. Netrusov, Y.U., Spectral synthesis in spaces of smooth Junctions, Russian Acad. Dokl. Math. 46 (1993), 135–138.Google Scholar
15. Khrushshev, S. and Peller, V., Hankel operators, best approximation, and stationary Gaussian processes, Russian Math. Surveys, 37 (1982), 61–144.Google Scholar
16. Richter, S., Invariant subspaces in Banach spaces of analytic functions, Trans. Amer. Math. Soc. 304 (1987), 585–616.Google Scholar
17. Richter, S., Ross, W.T. and Sundberg, C., Hyperinvariant subspaces of the harmonic Dirichlet space, J. Reine. Angew. Math. 448 (1994), 1–26.Google Scholar
18. Richter, S. and Shields, A.L., Bounded analytic functions in the Dirichlet space, Math. Z. 198 (1988), 151–159.Google Scholar
19. Ross, W.T., Invariant subspaces of Bergman spaces on slit domains, Bull. London. Math. Soc. 26 (1994), 472–482.Google Scholar
20. Ross, W.T. The commutant of a certain compression, Proc. Amer. Math. Soc. 118 (1993), 831–837.Google Scholar
21. Ross, W.T., An invariant subspace problem for p = 1 Bergman spaces on slit domains, Integral Equations Operator Theory 20 (1994), 243–248.Google Scholar
22. Ross, W.T., Invariant subspaces of the harmonic Dirichlet space with large codimension, Proc. Amer. Math Soc, to appear.Google Scholar
23. Rubel, L.A. and Shields, A.L., The space of analytic junctions in a region, Ann. Inst. Fourier (Grenoble) 16 (1966), 235–277.Google Scholar
24. Rudin, W.,Functional Analysis, New York, McGraw-Hill, 1973.Google Scholar
25. Stein, E.M., The characterization of functions arising as potentials II, Bull. Amer. Math. Soc. 68 (1962), 577–582.Google Scholar
26. Vekua, I.N.,Generalized Analytic Functions, Reading, Addison-Wesley, 1962.Google Scholar