Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T17:42:57.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic K-Theory for Groups Acting on Ã2 Buildings

Published online by Cambridge University Press:  20 November 2018

Guyan Robertson  and
Tim Steger
Guyan Robertson
Affiliation:
Mathematics Department, University of Newcastle, Callaghan, NSW, 2308 Australia e-mail: [email protected]
Tim Steger
Affiliation:
Istituto Di Matematica e Fisica, Università degli Studi di, Sassari, Via Vienna 2, 07100 Sassari, Italia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\Gamma$ be a torsion free lattice in 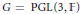$G=\text{PGL}\left( 3,\mathbb{F} \right)$ where $\mathbb{F}$ is a nonarchimedean local field. Then $\Gamma$ acts freely on the affine Bruhat-Tits building 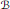$B$ of 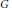$G$ and there is an induced action on the boundary 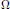$\Omega$ of 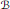$B$. The crossed product 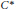${{C}^{*}}$ -algebra 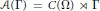$\mathcal{A}\left( \Gamma \right)=C\left( \Omega \right)\rtimes \Gamma$ depends only on $\Gamma$ and is classified by its $K$-theory. This article shows how to compute the $K$-theory of 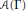$\mathcal{A}\left( \Gamma \right)$ and of the larger class of rank two Cuntz-Krieger algebras.

Keywords

46L8051E24K-theoryC*-algebraaffine building
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 4 , 01 August 2001 , pp. 809 - 833
Copyright
Copyright © Canadian Mathematical Society 2001

References

[BCH] Baum, P., Connes, A. and Higson, N., Classifying space for proper actions and K-theory of group C*-algebras. In: C*-algebras 1943–1993, A Fifty Year Celebration, 241–291, Contemporary Math. 167, Amer. Math. Soc., 1994.Google Scholar
[BBV] Béguin, C., Bettaieb, H. and Valette, A., K-theory for C*-algebras of one-relator groups. K-Theory 16(1999), 277–298.Google Scholar
[Bl] Blackadar, B., K-theory for Operator Algebras, Second Edition. MSRI Publications 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[Br1] Brown, K., Cohomology of Groups. Springer-Verlag, New York, 1982.Google Scholar
[Br2] Brown, K., Buildings. Springer-Verlag, New York, 1989.Google Scholar
[Br3] Brown, K., Five lectures on buildings. Group Theory from a Geometrical Viewpoint, Trieste, 1990, 254–295, World Sci. Publishing, River Edge, N.J., 1991.Google Scholar
[BV] Bettaieb, H. et Valette, A., Sur le groupe K 1 des C*-algèbres réduites de groupes discrets. C. R. Acad. Sci. Paris Sér. I Math. 322(1996), 925–928.Google Scholar
[C1] Cuntz, J., A class of C*-algebras and topological Markov chains: Reducible chains and the Ext-functor for C*-algebras. Invent. Math. 63(1981), 23–50.Google Scholar
[C2] Cuntz, J., K-theory for certain C*-algebras. Ann. of Math. 113(1981), 181–197.Google Scholar
[CK] Cuntz, J. and Krieger, W., A class of C*-algebras and topological Markov chains. Invent.Math. 56(1980), 251–268.Google Scholar
[Ca] Cartwright, D. I., Harmonic functions on buildings of type Ãn. Random Walks and Discrete Potential Theory, Cortona, 1997, 104–138, Symposia Mathematica XXXIX, Cambridge University Press, 1999.Google Scholar
[CMS] Cartwright, D. I., Młotkowski, W. and Steger, T., Property (T) and Ã2 groups. Ann. Inst. Fourier 44(1994), 213–248.Google Scholar
[CMSZ] Cartwright, D. I., Mantero, A. M., Steger, T. and Zappa, A., Groups acting simply transitively on the vertices of a building of type à 2 , I, II. Geom. Dedicata 47(1993), 143–166 and 167–223.Google Scholar
[EN] Elliott, G. and Natsume, T., A Bott periodicity map for crossed products of C*-algebras by discrete groups. K-Theory 1(1987), 423–435.Google Scholar
[Fu] Fuchs, L., Infinite Abelian Groups, vol. I. Academic Press, New York, 1970.Google Scholar
[Ka] Kasparov, G. G., Equivariant KK-theory and the Novikov conjecture. Invent.Math. 91(1988), 147–201.Google Scholar
[KaS] Kasparov, G. G. and Skandalis, G., Groups acting on buildings, operator K-theory, and Novikov's conjecture. K-Theory 4(1991), 303–337.Google Scholar
[Kir] Kirchberg, E., The classification of purely infinite C*-algebras using Kasparov's theory. In: Lectures in Operator Algebras, Fields Institute Monographs, Amer. Math. Soc., 1998.Google Scholar
[KR] Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, Volume II. Academic Press, New York, 1986.Google Scholar
[KL] Kleiner, B. and Leeb, B., Rigidity of quasi-isometries for symmetric spaces and Euclidean buildings. Inst. Hautes Études Sci. Publ. Math. 86(1997), 115–197.Google Scholar
[La] Lafforgue, V., Une démonstration de la conjecture de Baum-Connes pour les groupes réductifs sur un corps p-adique et pour certains groupes discrets possédant la propriété (T). C. R. Acad. Sci. Paris Sér. I Math. 327(1998), 439–444.Google Scholar
[Mar] Margulis, G. A., Discrete subgroups of semisimple Lie groups. Springer-Verlag, Berlin, 1991.Google Scholar
[Ph] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5(2000), 49–114.Google Scholar
[RS1] Robertson, G. and Steger, T., C*-algebras arising from group actions on the boundary of a triangle building. Proc. LondonMath. Soc. 72(1996), 613–637.Google Scholar
[RS2] Robertson, G. and Steger, T., Affine buildings, tiling systems and higher rank Cuntz-Krieger algebras. J. Reine Angew. Math. 513(1999), 115–144.Google Scholar
[RS3] Robertson, G. and Steger, T., K-theory computations for boundary algebras of Ã2 groups. http://maths.newcastle.edu.au/∼guyan/Kcomp.ps.gz Google Scholar
[Ron] Ronan, M., Lectures on Buildings. Perspect. Math. 7, Academic Press, New York, 1989.Google Scholar
[Ror] Rordam, M., Classification of Cuntz-Krieger algebras. K-Theory 9(1995), 31–58.Google Scholar
[Ser] Serre, J.-P., Arbres, amalgames, SL2. Astérisque 46, Soc. Math. France, 1977.Google Scholar
[Sp] Spanier, E. H., Algebraic topology. Springer-Verlag, New York, Berlin, 1981.Google Scholar
[St] Steger, T., Local fields and buildings. Harmonic Functions on Trees and Buildings, New York, 1995, 79–107, Contemporary Math. 206, Amer. Math. Soc., 1997.Google Scholar
[Tu] Tu, J.-L., The Baum-Connes conjecture and discrete group actions on trees. K-Theory 17(1999), 303–318.Google Scholar
[W] Weibel, C. A., An Introduction to Homological Algebra. Cambridge Studies in Advanced Math. 38, Cambridge University Press, Cambridge, 1994.Google Scholar
[WO] Wegge-Olsen, N. E., K-theory and C*-algebras: A Friendly Approach. Oxford University Press, Oxford, 1993.Google Scholar