Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T02:09:04.166Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Expansion of a Class of Multi-Dimensional Integrals

Published online by Cambridge University Press:  20 November 2018

A. Sellier
A. Sellier*
Affiliation:
LADHYX Ecole polytechnique 91128 Palaiseau Cedex France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to derive the expansion of the following class of multi-dimensional integrals

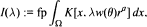
with respect to the large parameter λ when Ω is a subset of ℝn, a > 0, w is a strictly positive and bounded function on Σ and fp means an integration in the finite part sense of Hadamard (see Section 2). This is performed for weak assumptions bearing on pseudofunction K and by extending to higher dimensional cases the tools developed in the one-dimensional context. The range of applications of the proposed results is outlined by the exhibition of several examples.

Keywords

41A6041A60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 5 , 01 October 1996 , pp. 1079 - 1090
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Barlet, P., Développement asymptotique des fonctions obtenues sur les fibres, Invent., Math 68(1982), 129–174.Google Scholar
2. Bleistein, N. and Handelsman, R.A., Asymptotic Expansions of Integrals, Holt, Rinehart and Winston, New York, 1975.Google Scholar
3. Bruning, J., On the asymptotic expansion of some integrals, Arch., Math. 42(1984), 253–259.Google Scholar
4. Estrada, R. and Kanwal, R.P., The asymptotic expansion of certain multi-dimensional generalized functions, J. Math. Anal., Appl. 163(1992), 264–283.Google Scholar
5. Estrada, R., Asymptotic Analysis, A distributional Approach, Boston, Birkhauser, 1994.Google Scholar
6. Hadamard, J., Lectures on Cauchy's problem in linear differential equations, New York, Dover, 1932.Google Scholar
7. Malgrange, B., Integrales asymptotiques et monodromie, Ann. Sci. Ecole Norm. Sup., (4) 7(1974), 405- 430.Google Scholar
8. McClure, J.P. and Wong, R., Asymptotic expansion of a multiple integral, SIAM.J. Math., Anal. 18(1987), 1630–1637.Google Scholar
9. Schwartz, L., Theorie des Distributions, Paris, Hermann, 1966.Google Scholar
10. Sellier, A., Asymptotic expansions of a class of Integrals, Proc. Roy. Soc. London Ser., A 445(1994), 693–710.Google Scholar
11. Sellier, A., An alternative Method for the Asymptotic expansion of a double integral, J. Math. Anal., Appl. 194(1995), 741–762.Google Scholar
12. Wong, R., Asymptotic Approximations of Integrals, Boston, Academic Press, 1989.Google Scholar