No CrossRef data available.
Article contents
An Independent System of Units in Certain Algebraic Number Fields
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For Kn = Q(ω) a real algebraic number field of degree n over Q such that
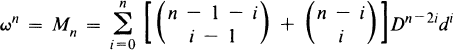
with D ∊ N, d ∊ Z, d|D2, and D2 + 4d > 0, we proved in [5] (by using the approach of Halter-Koch and Stender [6]) that if
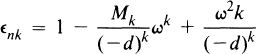
with
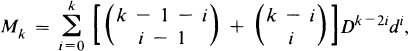
then
is an independent system of units of Kn.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
1.
Bernstein, L., Periodical continued fractions of degree n by Jacobi's algorithm,
J. reine angew. Math.
213 (1964), 31–38.Google Scholar
2.
Bernstein, L., Representation of 
as a periodic continued fraction by JacobVs algorithm, Math. Nachr.
29 (1965), 179–200.Google Scholar
as a periodic continued fraction by JacobVs algorithm, Math. Nachr.
29 (1965), 179–200.Google Scholar4.
Frei, G. and Levesque, C., On an independent system of units in the field where d|Dn, Abh. Math. Sem. Univ. Hamburg
51 (1980), 160–163.Google Scholar
where d|Dn, Abh. Math. Sem. Univ. Hamburg
51 (1980), 160–163.Google Scholar5.
Frei, G. and Levesque, C., Independent systems of units in certain algebraic number fields,
J. reine angew. Math.
311/312 (1979), 116–144.Google Scholar
6.
Halter-Koch, F. und Stender, H.-J., Unabhangige Einheiten für die Körper , Abh. Math. Sem. Univ. Hamburg
42 (1974), 33–40.CrossRefGoogle Scholar
, Abh. Math. Sem. Univ. Hamburg
42 (1974), 33–40.CrossRefGoogle Scholar7.
Stender, H.-J., Lösbare Gleichungen axn − byn = c und Grundeinheiten für einige algebraische Zahlkörper vom Grade n = 3, 4, 6, J. reine angew. Math.
290 (1977), 24–62.Google Scholar
You have
Access