Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-22T13:33:42.541Z Has data issue: false hasContentIssue false
  • English
  • Français

On commutators of square-zero Hilbert space operators

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  17 February 2025

Laurent W. Marcoux Open the ORCID record for Laurent W. Marcoux [Opens in a new window] ,
Heydar Radjavi  and
Yuanhang Zhang Open the ORCID record for Yuanhang Zhang [Opens in a new window]
Laurent W. Marcoux
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada, N2L 3G1 e-mail: [email protected]
Heydar Radjavi
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada, N2L 3G1 e-mail: [email protected]
Yuanhang Zhang*
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, People’s Republic of China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 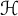$\mathcal H$ be a complex, separable Hilbert space, and set 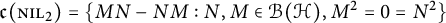. When 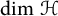$\dim \, \mathcal H$ is finite, we characterise the set 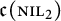and its norm-closure 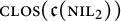. In the infinite-dimensional setting, we characterise the intersection of 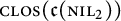with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to .

Keywords

Commutatorsnilpotents of order twobiquasitriangular

MSC classification

Primary: 47B47: Commutators, derivations, elementary operators, etc.
Secondary: 47A58: Operator approximation theory
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 36
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

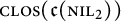Laurent W. Marcoux is supported in part by NSERC (Canada); Yuanhang Zhang is supported in part by National Natural Science Foundation of China (No.: 12071174)

References

Albert, A. A. and Muckenhoupt, B., On matrices of trace zero . Michigan Math. J. 3(1957), 1–3.Google Scholar
Anderson, J., Commutators of compact operators . J. Reine Angew. Math. 291(1977), 128–132.Google Scholar
Apostol, C., Fialkow, L. A., Herrero, D. A., and Voiculescu, D., Approximation of Hilbert space operators II, Research Notes in Mathematics, 102, Pitman Advanced Publishing Program, Boston, London, Melbourne, 1984.Google Scholar
Apostol, C., Foiaş, C., and Voiculescu, D., On the norm-closure of the nilpotents IV . Rev. Roumaine Math. Pures Appl. 18(1974), 487–514.Google Scholar
Barnes, B. A., Common operator properties of the linear operators $RS$ and $SR$ . Proc. Amer. Math. Soc. 126(1998), 1055–1061.CrossRefGoogle Scholar
Beltiţă, D., Patnaik, S., and Weiss, G., $\mathcal{B}(\mathcal{H})$ -commutators: a historical survey II and recent advances on commutators of compact operators, Theta Series in Advanced Mathematics, 17, Theta, Bucharest, 2014, pp. 57–75.Google Scholar
Borwein, J. M. and Richmond, B., How many matrices have roots? Can. J. Math. 36(1984), 286–299.CrossRefGoogle Scholar
Brown, A. and Pearcy, C., Structure of commutators of operators . Ann. of Math. (2) 82(1965), 112–127.CrossRefGoogle Scholar
Chen, K. Y., Herrero, D. A., and Wu, P. Y., Similarity and quasisimilarity of quasinormal operators . J. Operator Theory 27(1992), 385–412.Google Scholar
Conway, J. B., A course in functional analysis, 2nd ed., Graduate Texts in Mathematics, 96, Springer-Verlag, New York, 1990.Google Scholar
Davidson, K. R., ${C}^{\ast }$ -algebras by example, Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
Drnovšek, R., Radjavi, H., and Rosenthal, P., A characterization of commutators of idempotents . Linear Algebra Appl. 347(2002), 91–99.CrossRefGoogle Scholar
Dykema, K. and Krishnaswamy-Usha, M., Nilpotent elements of operator ideals as single commutators . Proc. Amer. Math. Soc. 146(2018), 3031–3037.CrossRefGoogle Scholar
Dykema, K. and Skripka, A., On single commutators in II ${}_1$ factors. Proc. Amer. Math. Soc. 140(2012), 931–940.CrossRefGoogle Scholar
Fack, T., Finite sums of commutators in ${C}^{\ast }$ -algebras . Ann. Inst. Fourier, Grenoble 32(1982), 129–137.CrossRefGoogle Scholar
Gellar, R., Operators commuting with a weighted shift . Proc. Amer. Math. Soc. 23(1969), 538–545.CrossRefGoogle Scholar
Halmos, P. R., A Hilbert space problem book, 2nd ed., Springer–Verlag, New York, 1982.CrossRefGoogle Scholar
Han, J. K., Lee, H. Y., and Lee, W. Y., Invertible completions of $2\times 2$ upper triangular operator matrices. Proc. Amer. Math. Soc. 128(2000), 119–123.CrossRefGoogle Scholar
Herrero, D. A., Approximation of Hilbert space operators I, 2nd ed., Pitman Research Notes in Mathematics Series, 224, Longman Scientific and Technical, Harlow, New York, 1989.Google Scholar
Herrero, D. A., A metatheorem on similarity and approximation of operators . J. Lond. Math. Soc. 42(1990), 535–554.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R., Matrix analysis, Cambridge University Press, Cambridge, New York, Melbourne, 1990.Google Scholar
Jiang, C. L. and Wang, Z. Y., Strongly irreducible operators on Hilbert space, Pitman Research Notes in Mathematics Series, 389, Longman, Harlow, 1998.Google Scholar
Kaftal, V., Ng, P. W., and Zhang, S., Commutators and linear spans of projections in certain finite ${C}^{\ast }$ -algebras . J. Funct. Anal. 266(2014), 1883–1912.CrossRefGoogle Scholar
Khatami, L., The poset of the nilpotent commutator of a nilpotent matrix . Linear Algebra Appl. 439(2013), 3763–3776.CrossRefGoogle Scholar
Marcoux, L. W., Sums of small numbers of commutators . J. Operator Theory 56(2006), 111–142.Google Scholar
Marcoux, L. W., Projections, commutators and Lie ideals in ${C}^{\ast }$ -algebras . Math. Proc. R. Ir. Acad. 110A(2010), 31–55.CrossRefGoogle Scholar
Marcoux, L. W., Radjavi, H., and Zhang, Y., Around the closure of the set of commutators of idempotent elements of $\mathcal{B}(\mathcal{H})$ : biquasitriangularity and factorisation . J. Funct. Anal. 284(2023), Paper no. 109854, 45 pp.CrossRefGoogle Scholar
Marcoux, L. W., Radjavi, H., and Zhang, Y., Around the closures of the set of commutators and the set of differences of idempotent elements of $\mathcal{B}(\mathcal{H})$ . J. Operator Theory 91(2024), no. 1, 97–124.Google Scholar
Novak, N., Products of square-zero operators . J. Math. Anal. Appl. 339(2008), 10–17.CrossRefGoogle Scholar
Oblak, P., On the nilpotent commutator of a nilpotent matrix . Linear Multilinear Algebra 60(2012), 599–612.CrossRefGoogle Scholar
Otero, D. E., Extraction of $m$ th roots in matrix rings over fields . Linear Algebra Appl. 128(1990), 1–26.CrossRefGoogle Scholar
Öztük Kaptanoğlu, S., Commuting nilpotent operators and maximal rank . Complex Anal. Oper. Theory 4(2010), 901–904.CrossRefGoogle Scholar
Öztük, S., On $m$ -th roots of nilpotent matrices. Electron. J. Linear Algebra 37(2021), 718–733.CrossRefGoogle Scholar
Psarrakos, P. J., On the $m$ th roots of a complex matrix . Electron. J. Linear Algebra 9(2002), 32–41.CrossRefGoogle Scholar
Radjavi, H. and Rosenthal, P., On commutators of idempotents . Linear Multilinear Algebra 50(2002), 121–124.CrossRefGoogle Scholar
Robert, L., Nuclear dimension and sums of commutators . Indiana Univ. Math. J. 64(2015), 559–576.CrossRefGoogle Scholar
Smith, J. H., Commutators of nilpotent matrices . Linear Multiilinear Algebra. 4(1976), 17–19.CrossRefGoogle Scholar
Weiss, G., Commutators of Hilbert-Schmidt operators II . Integral Equations Operator Theory 3(1980), 574–600.CrossRefGoogle Scholar
Weiss, G., Commutators of Hilbert-Schmidt operators I . Integral Equations Operator Theory 9(1986), 877–892.CrossRefGoogle Scholar
Weiss, G., $\mathcal{B}(\mathcal{H})$ -commutators, recent advances in operator theory, Operator Theory: Advances and Applications, 153, Birkhäuser Verlag, Basel, 2005, pp. 307–320.Google Scholar
Yood, B., Rootless matrices . Math. Mag. 75(2002), 219–223.CrossRefGoogle Scholar