Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T07:17:37.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Global existence of a weak solution for a reaction–diffusion system in a porous medium with membrane conditions and mass control

Part of: Representations of solutions Equations of mathematical physics and other areas of application Parabolic equations and systems

Published online by Cambridge University Press:  20 November 2024

Safimba Soma Open the ORCID record for Safimba Soma [Opens in a new window] ,
Siaka Kambele  and
Aboudramane Guiro
Safimba Soma*
Affiliation:
Laboratoire de Mathématiques et d’Informatique (LA.M.I), UFR, Sciences Exactes et Appliquées, Université Joseph KI-ZERBO, 03 BP 7021 Ouagadougou 03, Burkina Faso
Siaka Kambele
Affiliation:
Laboratoire de Mathématiques et d’Informatique (LA.M.I), UFR, Sciences Exactes et Appliquées, Université Joseph KI-ZERBO, 03 BP 7021 Ouagadougou 03, Burkina Faso e-mail: [email protected]
Aboudramane Guiro
Affiliation:
Laboratoire de Mathématiques, d’Informatique et Applications (LaMIA), UFR, Sciences Exactes et Appliquées, Université Nazi BONI, 01 BP 1091 Bobo 01, Bobo Dioulasso, Burkina Faso e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the global exstence of weak solutions for a porous medium dynamics of m species moving between two domains separated by a zero-thickness membrane. On this membrane, Kedem–Katchalsky conditions are considered, and the study is characterized by natural structural conditions applied to the nonlinear reactive terms. The global existence is established under the assumption that these reactive terms are bounded in 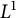$L^1$. This problem has already been analyzed in the linear diffusion case by Ciavolella and Perthame in Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540). The present work constitutes an extension for nonlinear diffusion, particularly of the porous medium type, in the form 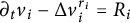$\partial _t v_i - \Delta v_i^{r_i} = R_i$, for an exponent 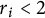$r_i < 2$. The case 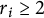$r_i \geq 2$ remains an open problem. This paper is an adaptation of the ideas from Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540), with new strategies to overcome the appearance of nonlinearity and degeneracy in the diffusion term.

Keywords

Kedem–Katchalsky conditionsmembrane boundary conditionsreaction–diffusion systemglobal existencenonlinear diffusion

MSC classification

Primary: 35K10: Second-order parabolic equations 35K40: Second-order parabolic systems 35K57: Reaction-diffusion equations 35D30: Weak solutions 35Q92: PDEs in connection with biology and other natural sciences
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 23
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdellaoui, B., Peral, I., and Walias, M., Some existence and regularity results for porous media and fast diffusion equations with a gradient term . Trans. Amer. Math. Soc. 367(2015), no. 7, 4757–4791.CrossRefGoogle Scholar
Baras, P., Compacité de l’opérateur $f\mapsto u$ solution d’une équation non-linéaire   $\frac{du}{dt}+ Au\ni f$ . C. R. Acad. Sci. 286(1978), 1113–1116.Google Scholar
Baras, P. and Pierre, M., Problems paraboliques semi-lineaires avec donnees measures . Appl. Anal. 18(1984), nos. 1–2, 111–149.CrossRefGoogle Scholar
Bathory, M., Bulíček, M., and Souček, O., Existence and qualitative theory for nonlinear elliptic systems with a nonlinear interface condition used in electrochemistry . Z. Angew. Math. Phys. 71(2020), no. 3, 74.CrossRefGoogle Scholar
Bothe, D. and Pierre, M., Quasi-steady-state approximation for a reaction–diffusion system with fast intermediate . J. Math. Anal. Appl. 368(2010), no. 1, 120–132.CrossRefGoogle Scholar
Calabrò, F. and Zunino, P., Analysis of parabolic problems on partitioned domains with nonlinear conditions at the interface: application to mass transfer through semi-permeable membranes . Math. Models Methods Appl. Sci. 16(2006), no. 4, 479–501.CrossRefGoogle Scholar
Cangiani, A. and Natalini, R., A spatial model of cellular molecular trafficking including active transport along microtubules . J. Theor. Biol. 267(2010), no. 4, 614–625.CrossRefGoogle ScholarPubMed
Cañizo, J., Desvillettes, L., and Fellner, K., Improved duality estimates and applications to reaction–diffusion equations . Commun. Partial Differ. Equ. 39(2014), no. 6, 1185–1204.CrossRefGoogle Scholar
Chaplain, M. A., Giverso, C., Lorenzi, T., and Preziosi, L., Derivation and application of effective interface conditions for continuum mechanical models of cell invasion through thin membranes . SIAM J. Appl. Math. 79(2019), no. 5, 2011–2031.CrossRefGoogle Scholar
Ciavolella, G. and Perthame, B., Existence of a global weak solution for a reaction–diffusion problem with membrane conditions . J. Evol. Equ. 21(2021), no. 2, 1513–1540.CrossRefGoogle Scholar
Desvillettes, L., Fellner, K., Pierre, M., and Vovelle, J., Global existence for quadratic systems of reaction-diffusion . Adv. Nonlinear Stud. 7(2007), no. 3, 491–511.CrossRefGoogle Scholar
Fonseca, I. and Leoni, G., Modern methods in the calculus of variations: Lp-spaces, Springer Science & Business Media, New York, 2007.Google Scholar
Gallinato, O., Colin, T., Saut, O., and Poignard, C., Tumor growth model of ductal carcinoma: from in situ phase to stroma invasion . J. Theor. Biol. 429(2017), 253–266.CrossRefGoogle ScholarPubMed
Hollis, S. L., Martin, R. H., and Pierre, M., Global existence and boundedness in reaction–diffusion systems . SIAM J. Math. Anal. 18(1987), no. 3, 744–761.CrossRefGoogle Scholar
Kanel, J. I. and Kirane, M., Global solutions of reaction–diffusion systems with a balance law and nonlinearities of exponential growth . J. Differ. Equ. 165(2000), no. 1, 24–41.CrossRefGoogle Scholar
Kedem, O. and Katchalsky, A., A physical interpretation of the phenomenological coefficients of membrane permeability . J. Gen. Physiol. 45(1961), no. 1, 143–179.CrossRefGoogle ScholarPubMed
Kouachi, S., Existence of global solutions to reaction–diffusion systems via a Lyapunov functional . Electron. J Differential Equations 2001(2001), Article no. 68, 10 pp.Google Scholar
Laamri, E. H.. Existence globale pour des systèmes de réaction-diffusion dans ${L}^1$ . PhD thesis, Université Nancy 1, 1988.Google Scholar
Laamri, E. H. and Perthame, B., Reaction–diffusion systems with initial data of low regularity . J. Differ. Equ. 269(2020), no. 11, 9310–9335.CrossRefGoogle Scholar
Laamri, E. H. and Pierre, M., Global existence for reaction–diffusion systems with nonlinear diffusion and control of mass . Ann. Inst. H. Poincaré Anal. Non linéaire. 34(2017), 571–591.CrossRefGoogle Scholar
Li, J., Su, L., Wang, X., and Wang, Y., Bulk-surface coupling: derivation of two models . J. Differ. Equ. 289(2021), 1–34.CrossRefGoogle Scholar
Lukkari, T., The porous medium equation with measure data . J. Evol. Equ. 10(2010), 711–729.CrossRefGoogle Scholar
Lukkari, T., The fast diffusion equation with measure data . NoDEA Nonlinear Differential Equations Appl. 19(2012), no. 3, 329–343.CrossRefGoogle Scholar
Martin, R. H. and Pierre, M., Nonlinear reaction–diffusion systems , Math. Sci. Eng. 185(1992), 363–398.CrossRefGoogle Scholar
Masuda, K., On the global existence and asymptotic behavior of solutions of reaction–diffusion equations . Hokkaido Math. J. 12(1983), no. 3, 360–370.CrossRefGoogle Scholar
Morgan, J., Global existence for semilinear parabolic systems . SIAM J. Math. Anal. 20(1989), no. 5, 1128–1144.CrossRefGoogle Scholar
Pierre, M., Weak solutions and supersolutions in ${l}^1$ for reaction–diffusion systems . J. Evol. Equ. 1(2003), no. 3, 153–168.CrossRefGoogle Scholar
Pierre, M., Global existence in reaction–diffusion systems with control of mass: a survey . Milan J. Math. 78(2010), 417–455.CrossRefGoogle Scholar
Pierre, M. and Schmitt, D., Blowup in reaction–diffusion systems with dissipation of mass . SIAM Rev. 42(2000), no. 1, 93–106.CrossRefGoogle Scholar
Prüss, J., Maximal regularity for evolution equations in Lp-spaces . Conf. Semin. Mat. Univ. Bari. 285(2002), 1–39.Google Scholar
Quarteroni, A., Veneziani, A., and Zunino, P., Mathematical and numerical modeling of solute dynamics in blood flow and arterial walls . SIAM J. Numer. Anal. 39(2002), no. 5, 1488–1511.CrossRefGoogle Scholar
Quittner, P. and Souplet, P., Superlinear parabolic problems: blow-up, global existence and steady states, Springer Science & Business Media, Berlin, 2007.Google Scholar
Schilling, R. L., Measures, integrals and martingales, Cambridge University Press, Cambridge, 2017.Google Scholar
Serafini, A.. Mathematical models for intracellular transport phenomena. PhD in Applied Mathematics, Universita degli Studi di Roma “La Sapienza,” Dottorato di Ricerca in Modelli e Metodi Matematici per la tecnologia e la societa, 2007.Google Scholar
Vázquez, J. L., The porous medium equation: mathematical theory, Clarendon Press, Oxford, 2006.CrossRefGoogle Scholar