Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-04-08T15:26:37.221Z Has data issue: false hasContentIssue false
  • English
  • Français

The 2-Sylow-Subgroup of the Tame Kernel of Number Fields

Published online by Cambridge University Press:  20 November 2018

Boris Brauckmann
Boris Brauckmann*
Affiliation:
Westf. Wilhelms-Universität Math. Institut Einsteinstr. 62 D-4400 Münster
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a number field F with ring of integers OF the tame symbols yield a surjective homomorphism 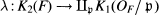with a finite kernel, which is called the tame kernel, isomorphic to K2(OF). For the relative quadratic extension E/F, where 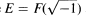and E ≠ F, let CS(E/ F)(2) denote the 2-Sylow-subgroup of the relative S-class-group of E over F, where S consists of all infinite and dyadic primes of F, and let m be the number of dyadic primes of F, which decompose in E.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 2 , 01 April 1991 , pp. 255 - 264
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Birch, J., K2 of global fields. Proc. Symp. Pure Math. 20 Providence, AMS, 1971, 87–95.Google Scholar
2. Brauckmann, B., 4-ranks of S-class-groups, preprint, 1989.Google Scholar
3. Browkin, J. and Hurrelbrink, J., On the generation ofK2(0) by symbols, LNM 1046(1984), 29–31.Google Scholar
4. Browkin, J. and Schinzel, A., On Sylow 2-subgroups ofK2 (0F) for quadratic number fields F, Journal Reine Angewandte Mathematik 331(1982), 104–113.Google Scholar
5. Brown, E., Class numbers of complex quadratic fields, Journal of Number Theory 6(1974), 185–191.Google Scholar
6. Coates, J., On K2 and some classical conjectures in algebraic number theory, Ann. of Math. 95(1972), 99–116.Google Scholar
7. Coates, J., p-adic L-functions andIwasawa's theory. Fröhlich, A. (ed.): Algebraic Number Fields, Academic Press, London (1977), 269–353.Google Scholar
8. Conner, P.E. and Hurrelbrink, J., Class number parity, to appear in Series in Pure Mathematics, World Scientific Publishing Co., Singapore, 1988.Google Scholar
9. Conner, P.E. and Hurrelbrink, J., On the 4-rank of the tame kernel, preprint, 1988.Google Scholar
10. Fédérer, L.J., Regulators, Iwasawa modules and the main conjecture for p = 2. N. Koblitz (éd.): Number Theory related to Fermat's last theorem, Birkhäuser, Basel (1982), 289–296.Google Scholar
11. Halter-Koch, F., Über den 4-Rang der Klassengruppe quadraticher Zahlkörper, Journal of Number Theory 19(1984), 219–227.Google Scholar
12. Hasse, H., Über die Klassenzahl des Körpers mit einer Primzahlp ≠ 2, Journal of Number theory 1(1969), 231–234.Google Scholar
13. Hasse, H., Über die Klassenzahl des Körpers mit einer Primzahl p = 1 mod 23, Aeq. Math. 3 ( 1969), 165–169.Google Scholar
14. Hasse, H., Über die Klassenzahl abelscher Zahlhorper. Akademie-Verlag Berlin, 1952, new edition, Springer, 1985.Google Scholar
15. Kolster, M., The structure of the 2-Sylow-subgroup of K2 (0), I, Comment. Math. Helvetici 61(1986), 376- 388.Google Scholar
16. Kolster, M., The structure of the 2-Sylow-subgroup of K2 (0),II, K-Theory 1(1987), 467–479.Google Scholar
17. Kolster, M., A relation between the 2-primary parts of the Main Conjecture and the Birch-Tate Conjecture, preprint, 1988.Google Scholar
18. Pizer, A., On the 2-part of class numbers of imaginary quadratic numberfields, Journal of Number Theory 8(1976), 184–192.Google Scholar
19. Redei, L. and Reichardt, H., Die Anzahl der durch 4 teilbaren Invarianten der Klassengruppe eines beliebigen quadratischen Zahlkörpers, Journal Reine Angewandte Mathematik 170(1934), 69–74.Google Scholar
20. Tate, J., Symbols in arithmetic, Act. Congr. int. math., Nizza 1970.Google Scholar
21. Wiles, A., The Iwasawa conjecture for totally real fields, Ann. of Math. 131(1990), 493–570.Google Scholar