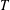 $T$-GAIN SPECTRA
$T$-GAIN SPECTRA
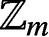 $\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
$\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
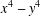 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
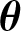 $\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
$\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
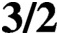 $\textbf{3/2}$
ETA-PRODUCTS
$\textbf{3/2}$
ETA-PRODUCTS