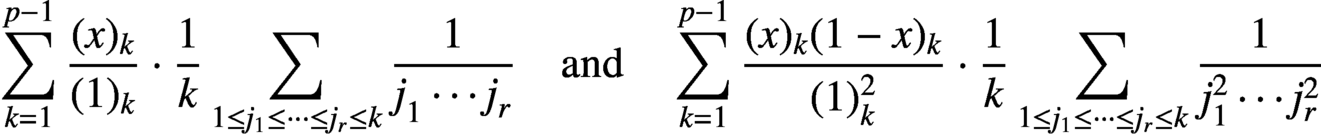Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-26T01:56:22.710Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  28 January 2021

ROBERTO TAURASO Open the ORCID record for ROBERTO TAURASO [Opens in a new window]
ROBERTO TAURASO*
Affiliation:
Dipartimento di Matematica, Università di Roma ‘Tor Vergata’, via della Ricerca Scientifica 1, 00133Roma, Italy
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let p be a prime and let x be a p-adic integer. We prove two supercongruences for truncated series of the form

$$\begin{align*}\sum_{k=1}^{p-1} \frac{(x)_k}{(1)_k}\cdot \frac{1}{k}\sum_{1\le j_1\le\cdots\le j_r\le k}\frac{1}{j_1^{}\cdots j_r^{}}\quad\mbox{and}\quad \sum_{k=1}^{p-1} \frac{(x)_k(1-x)_k}{(1)_k^2}\cdot \frac{1}{k}\sum_{1\le j_1\le\cdots\le j_r\le k}\frac{1}{j_1^{2}\cdots j_r^{2}}\end{align*}$$
which generalise previous results. We also establish q-analogues of two binomial identities.

Keywords

Bernoulli numbercentral binomial coefficientcongruenceharmonic sum

MSC classification

Primary: 11B65: Binomial coefficients; factorials; $q$-identities
Secondary: 11A07: Congruences; primitive roots; residue systems 11B68: Bernoulli and Euler numbers and polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 379 - 389
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Hernández, V., ‘Solution IV of problem 10490: a reciprocal summation identity’, Amer. Math. Monthly 106 (1999), 589–590.Google Scholar
Pilehrood, Kh. Hessami, Pilehrood, T. Hessami and Tauraso, R., ‘New properties of multiple harmonic sums modulo $p$ and $p$ -analogues of Leshchiner’s series’, Trans. Amer. Math. Soc. 366 (2014), 3131–3159.CrossRefGoogle Scholar
Prodinger, H., ‘A $q$ -analogue of a formula of Hernández obtained by inverting a result of Dilcher’, Australas. J. Combin. 21 (2000), 271–274.Google Scholar
Prodinger, H., ‘Identities involving harmonic numbers that are of interest for physicists’, Util. Math. 83 (2010), 291–299.Google Scholar
Sun, Z.-H., ‘Congruences concerning Bernoulli numbers and Bernoulli polynomials’, Discrete Appl. Math. 105 (2000), 193–223.CrossRefGoogle Scholar
Sun, Z.-H., ‘Generalized Legendre polynomials and related supercongruences’, J. Number Theory 143 (2014), 293–319.CrossRefGoogle Scholar
Sun, Z.-H., ‘Super congruences concerning Bernoulli polynomials’, Int. J. Number Theory 11 (2015), 2393–2404.CrossRefGoogle Scholar
Sun, Z.-W., ‘A new series for ${\pi}^3$ and related congruences’, Internat. J. Math. 26 (2015), 1550055, 23 pages.CrossRefGoogle Scholar
Tauraso, R., ‘Congruences involving alternating multiple harmonic sums’, Electron. J. Combin. 17 (2010), R16, 11 pages.CrossRefGoogle Scholar
Tauraso, R., ‘Supercongruences for a truncated hypergeometric series’, Integers 12 (2012), A45, 12 pages.Google Scholar
Zhao, J., ‘Bernoulli numbers, Wolstenholme’s theorem, and ${p}^5$ variations of Lucas’ theorem’, J. Number Theory 123 (2007), 18–26.CrossRefGoogle Scholar