Research Article
Integration by parts for some general integrals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-15
-
- Article
-
- You have access
- Export citation
Rings in which every element is the sum of two idempotents
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-164
-
- Article
-
- You have access
- Export citation
Jordan derivations on prime rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-322
-
- Article
-
- You have access
- Export citation
Some representation formulae for entire functions of exponential type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 17-26
-
- Article
-
- You have access
- Export citation
On the weak*-Radon Nikodym property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 323-332
-
- Article
-
- You have access
- Export citation
On the generalised dominated convergence theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 165-171
-
- Article
-
- You have access
- Export citation
Singleton arrays in coding theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 333-335
-
- Article
-
- You have access
- Export citation
Structure presque-transverse intégrable
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 173-177
-
- Article
-
- You have access
- Export citation
On quadratic functionals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 27-28
-
- Article
-
- You have access
- Export citation
Fourth-order boundary value problems at nonresonance
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-343
-
- Article
-
- You have access
- Export citation
Bifurcations of second order problems with jumping nonlinearities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-187
-
- Article
-
- You have access
- Export citation
Demicontinuity of Nemitsky operators on Orlicz-Sobolev spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 29-42
-
- Article
-
- You have access
- Export citation
Injectivity and injective hulls of Abelian groups in a localic topos
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-59
-
- Article
-
- You have access
- Export citation
On cyclic group actions of even order on the three dimensional torus
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-196
-
- Article
-
- You have access
- Export citation
A linear complementarity problem involving a subgradient
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-351
-
- Article
-
- You have access
- Export citation
Elementary equivalence and genus of finitely generated nilpotent groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 61-68
-
- Article
-
- You have access
- Export citation
Monochromatic triangles in three colours
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-212
-
- Article
-
- You have access
- Export citation
Integrally closed factor domains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-366
-
- Article
-
- You have access
- Export citation
Groups with a nilpotent triple factorisation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-79
-
- Article
-
- You have access
- Export citation
Multiobjective fractional duality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-378
-
- Article
-
- You have access
- Export citation

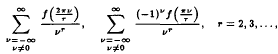
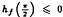 in the first case). These series are expressed in terms of the derivatives of
in the first case). These series are expressed in terms of the derivatives of