This paper produces new types of designs, called product designs, which prove extremely useful for constructing orthogonal designs. An orthogonal design of order 2t and type
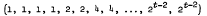
is constructed. This design often meets the Radon bound for the number of variables.
We also show that all orthogonal designs of order 2t and type (a, b, c, d, 2t-a-b-c-d), with 0 < a + b + c + d < 2t, exist for t = 5, 6, and 7.