Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-10T04:59:27.871Z Has data issue: false hasContentIssue false
  • English
  • Français

A result on tournaments with an application to counting

Published online by Cambridge University Press:  17 April 2009

W.J.R. Eplett
W.J.R. Eplett
Affiliation:
Department of Applied Mathematics, University of the Witwatersrand, Johannesburg, South Africa.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A generating function is derived for the number of transitions to the first passage through a particular vertex of a random walk on a doubly regular tournament. As an application of this result, we obtain a generating function for the number of solutions (q1, …, qk) of 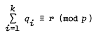qi ≡ r (mod p), where p is a prime of the form 4l + 3 and the qi are quadratic residues modulo p.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 16 , Issue 2 , April 1977 , pp. 273 - 278
Copyright
Copyright © Australian Mathematical Society 1977

References

[1]Chowla, S., The Riemann hypothesis and Hilbert's tenth problem (Mathematics and its Applications, 4. Gordon and Breach, New York, London, Paris, 1965).Google Scholar
[2]Moon, John W., Tapics on tournaments (Holt, Rinehart and Winston, New York, Chicago, San Francisco, Atlanta, Dallas, Montreal, Toronto, London, 1968).Google Scholar
[3]Ryser, Herbert John, Combinatorial mathematics (Carus Mathematical Monographs, 14. Mathematical Association of America, N.P., 1963).CrossRefGoogle Scholar
[4]Williams, K.S., “On a result of Libri and Lebesgue”, Amer. Math. Monthly 77 (1970), 610–613.CrossRefGoogle Scholar