For any pair of integers p, q such that (p, q) = 1 and p ≥ 2q, the graph 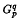 has vertices {0, 1, …, p − 1} and edges {ij: q ≤ |i − j| ≤ p − q}. These graphs play the same role in the study of circular chromatic number as that played by the complete graphs in the study of chromatic number. The graphs
has vertices {0, 1, …, p − 1} and edges {ij: q ≤ |i − j| ≤ p − q}. These graphs play the same role in the study of circular chromatic number as that played by the complete graphs in the study of chromatic number. The graphs 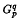 share many properties of the complete graphs. However, there are also striking differences between the graphs
share many properties of the complete graphs. However, there are also striking differences between the graphs 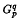 and the complete graphs. We shall prove in this paper that for many pairs of integers p, q, one may delete most of the edges of
and the complete graphs. We shall prove in this paper that for many pairs of integers p, q, one may delete most of the edges of 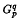 so that the resulting graph still has circular chromatic number p/q. To be precise, we shall prove that for any number r < 2, there exists a rational number p/q (where (p, q) = 1) which is less than r but arbitrarily close to r, such that
so that the resulting graph still has circular chromatic number p/q. To be precise, we shall prove that for any number r < 2, there exists a rational number p/q (where (p, q) = 1) which is less than r but arbitrarily close to r, such that 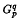 contains a subgraph H with
contains a subgraph H with 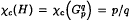 and
and 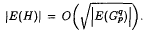 . This is in sharp contrast to the fact that the complete graphs are edge critical, that is, the deletion of any edge will decrease its chromatic number and its circular chromatic number.
. This is in sharp contrast to the fact that the complete graphs are edge critical, that is, the deletion of any edge will decrease its chromatic number and its circular chromatic number.