Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T06:20:14.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper semi continuity of attractors of delay differential equations in the delay

Published online by Cambridge University Press:  17 April 2009

Peter E. Kloeden
Peter E. Kloeden
Affiliation:
FB Mathematik, Johann Wolfgang Goethe Universität, D-60054 Frankfurt am Main, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

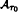It is shown that if a retarded delay differential equation has a global attractor in the space C ([—τ0, ], ℝd) for a given nonzero constant delay τ0, then the equation has an attractor Aτ in the space C ([—τ, 0], ℝd) for nearby constant delays τ. Moreover the attractors Aτ converge upper semi continuously to 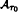in C ([—τ0, 0], ℝd) in the sense that they are identified through corresponding segments of entire trajectories in ℝd with nonempty compact subsets 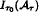of C ([—τ0, 0], ℝd) which converge upper semi continuously to 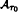in C ([—τ0, 0], ℝd).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 2 , April 2006 , pp. 299 - 306
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Driver, R.D., Ordinary and delay differential equations, Applied Mathematical Sciences 20 (Springer-Verlag, Heidelberg, 1977).CrossRefGoogle Scholar
[2]Hale, J.K., Asymptotic behavior of dissipative dynamical systems (Amer. Math. Soc., Providence, R.I., 1988).Google Scholar
[3]Hale, J.K. and Lunel, S.M. Verduyn, Introduction to functional differential equations (Springer-Verlag, Heidelberg, 1993).Google Scholar
[4]Kloeden, P.E. and Lorenz, J., ‘Stable attracting sets in dynamical systems and in their one-step discretizations’, SIAM J. Numer. Anal. 23 (1986), 986–993.Google Scholar
[5]Kloeden, P.E. and Schropp, J., ‘Stable attracting sets in delay differential equations and in their Runge-Kutta discretizations’, Numer. Funct. Anal. Optim. (to appear).Google Scholar
[6]Kloeden, P.E. and Siegmund, S., ‘Bifurcations and continuous transitions of attractors in autonomous and nonautonomous systems’, J. Bifur. Chaos. Appl. Sci. Engg. 15 (2005), 743–762.Google Scholar
[7]Yoshizawa, T., Stability theory by Lyapunov's second method, Publication of the Mathematical Society of Japan 9 (The Mathematical Society of Japan, Tokyo, 1966).Google Scholar