No CrossRef data available.
Published online by Cambridge University Press: 02 October 2020
Let E and D be open subsets of
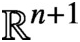 $\mathbb {R}^{n+1}$
such that
$\mathbb {R}^{n+1}$
such that
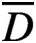 $\overline {D}$
is a compact subset of E, and let v be a supertemperature on E. A temperature u on D is called extendable by v if there is a supertemperature w on E such that
$\overline {D}$
is a compact subset of E, and let v be a supertemperature on E. A temperature u on D is called extendable by v if there is a supertemperature w on E such that
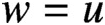 $w=u$
on D and
$w=u$
on D and
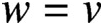 $w=v$
on
$w=v$
on
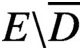 $E\backslash \overline D$
. From earlier work of N. A. Watson, [‘Extendable temperatures’, Bull. Aust. Math. Soc.100 (2019), 297–303], either there is a unique temperature extendable by v, or there are infinitely many; a necessary condition for uniqueness is that the generalised solution of the Dirichlet problem on D corresponding to the restriction of v to
$E\backslash \overline D$
. From earlier work of N. A. Watson, [‘Extendable temperatures’, Bull. Aust. Math. Soc.100 (2019), 297–303], either there is a unique temperature extendable by v, or there are infinitely many; a necessary condition for uniqueness is that the generalised solution of the Dirichlet problem on D corresponding to the restriction of v to
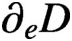 $\partial _eD$
is equal to the greatest thermic minorant of v on D. In this paper we first give a condition for nonuniqueness and an example to show that this necessary condition is not sufficient. We then give a uniqueness theorem involving the thermal and cothermal fine topologies and deduce a corollary involving only parabolic and coparabolic tusks.
$\partial _eD$
is equal to the greatest thermic minorant of v on D. In this paper we first give a condition for nonuniqueness and an example to show that this necessary condition is not sufficient. We then give a uniqueness theorem involving the thermal and cothermal fine topologies and deduce a corollary involving only parabolic and coparabolic tusks.