Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T20:06:58.345Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Complex dynamical systems Diophantine approximation, transcendental number theory Classical measure theory

Published online by Cambridge University Press:  02 November 2017

MUMTAZ HUSSAIN  and
WEILIANG WANG Open the ORCID record for WEILIANG WANG [Opens in a new window]
MUMTAZ HUSSAIN
Affiliation:
Department of Mathematics and Statistics, La Trobe University, PO Box 199, Bendigo 3552, Australia email [email protected]
WEILIANG WANG*
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074 Wuhan, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the two-dimensional shrinking target problem in beta-dynamical systems. Let 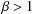$\unicode[STIX]{x1D6FD}>1$ be a real number and define the 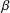$\unicode[STIX]{x1D6FD}$-transformation on 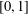$[0,1]$ by 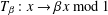$T_{\unicode[STIX]{x1D6FD}}:x\rightarrow \unicode[STIX]{x1D6FD}x\;\text{mod}\;1$. Let 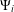$\unicode[STIX]{x1D6F9}_{i}$ (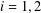$i=1,2$) be two positive functions on 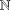$\mathbb{N}$ such that 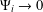$\unicode[STIX]{x1D6F9}_{i}\rightarrow 0$ when 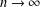$n\rightarrow \infty$. We determine the Lebesgue measure and Hausdorff dimension for the 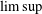$\limsup$ set

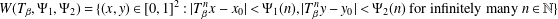$$\begin{eqnarray}W(T_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6F9}_{1},\unicode[STIX]{x1D6F9}_{2})=\{(x,y)\in [0,1]^{2}:|T_{\unicode[STIX]{x1D6FD}}^{n}x-x_{0}|<\unicode[STIX]{x1D6F9}_{1}(n),|T_{\unicode[STIX]{x1D6FD}}^{n}y-y_{0}|<\unicode[STIX]{x1D6F9}_{2}(n)\text{ for infinitely many }n\in \mathbb{N}\}\end{eqnarray}$$
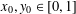for any fixed $x_{0},y_{0}\in [0,1]$.

Keywords

beta-expansionsshrinking target problemdynamical Borel–Cantelli lemmaHausdorff dimension

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 11J83: Metric theory 28A80: Fractals 37F35: Conformal densities and Hausdorff dimension
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 33 - 42
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Bugeaud, Y. and Wang, B., ‘Distribution of full cylinders and the Diophantine properties of the orbits in 𝛽-expansions’, J. Fractal Geom. 1 (2014), 799–827.Google Scholar
Chung, K., A Course in Probability Theory, 2nd edn, Probability and Mathematical Statistics, 21 (Academic Press, New York, 1974).Google Scholar
Coons, M., Hussain, M. and Wang, B., ‘A dichotomy law for the Diophantine properties in 𝛽-dynamical systems’, Mathematika 62(3) (2016), 884–897.Google Scholar
Dodson, M. M., ‘A note on metric inhomogeneous Diophantine approximation’, J. Aust. Math. Soc. Ser. A 62(2) (1997), 175–185.Google Scholar
Falconer, K., Fractal Geometry, Mathematical Foundations and Applications, 2nd edn (John Wiley, Hoboken, NJ, 2003).CrossRefGoogle Scholar
Fan, A. and Wang, B., ‘On the lengths of basic intervals in beta expansions’, Nonlinearity 25(5) (2012), 1329–1343.Google Scholar
Ge, Y. and Lü, F., ‘A note on inhomogeneous Diophantine approximation in beta-dynamical system’, Bull. Aust. Math. Soc. 91 (2015), 34–40.Google Scholar
Parry, W., ‘On the 𝛽-expansions of real numbers’, Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Philipp, W., ‘Some metrical theorems in number theory’, Pacific J. Math. 20 (1967), 109–127.Google Scholar
Rényi, A., ‘Representations for real numbers and their ergodic properties’, Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.Google Scholar
Shen, L. and Wang, B., ‘Shrinking target problems for beta-dynamical system’, Sci. China Math. 56 (2013), 91–104.Google Scholar
Wang, B., Wu, J. and Xu, J., ‘Mass transference principle for lim sup sets generated by rectangles’, Math. Proc. Cambridge Philos. Soc. 158 (2015), 419–437.CrossRefGoogle Scholar