Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-18T16:01:53.683Z Has data issue: false hasContentIssue false
  • English
  • Français

Trajectories of set valued integrals

Published online by Cambridge University Press:  17 April 2009

Nikolaos S. Papageorgiou
Nikolaos S. Papageorgiou
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, Illinois 61801, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to study the trajectory multifunction Φ(·) determined by the indefinite set valued integral of a measurable Banach space valued multifunction F(·), that is for all t ∈ [0, T], 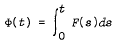, where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of SΦ equaling the set of selectors of Φ(·) whose primitive is an integrable selector of F(·). We also determine several useful properties that Φ(·) possesses and finally we present some convergence and stability results using the Kuratowski-Mosco convergence of sets.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 31 , Issue 3 , June 1985 , pp. 389 - 411
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Artstein, Z., “On the calculus of closed set valued functions”, Indiana Univ. Math. J. 24 (1974), 433–441.CrossRefGoogle Scholar
[2]Aumann, Robert J., “Integrals of set-valued functions”, J. Amth. Anal. Appl. 12 (1965), 1–12.Google Scholar
[3]Bradley, M. and Datko, R., “Some analytic and measure theoretic properties of set valued mappings”, SIAM J. Control Optim. 15 (1977), 625–635.CrossRefGoogle Scholar
[4]Bridgland, T.F. Jr., “Trajectory integrals of set valued functions”, Pacific J. Math. 33 (1970), 43–68.CrossRefGoogle Scholar
[5]Bridgland, J.F. Jr., “Extreme limits of compacta valued functions”, Trans. Amer. Math. Soc. 170 (1972), 149–163.CrossRefGoogle Scholar
[6]Castaing, Ch. and Valadier, M., Convex analysis and measurable multifunctions (Lecture Notes in Mathematics, 580. Springer-Verlag, Berlin, Heidelberg, New York, 1977).CrossRefGoogle Scholar
[7]Cornwall, R., “Conditions for the graph and the integral of a correspondence to be open”, J. Math. Anal. Appl. 39 (1972), 771–792.CrossRefGoogle Scholar
[8]Curtain, R. and Pritchard, A., Functional analysis in modern applied mathematics (Academic Press, New York, London, 1977).Google Scholar
[9]Diestel, J., “Remarks on weak compactness in L1(U; X)”, Glasgow Math. J. 18 (1977), 87–91.CrossRefGoogle Scholar
[10]Diestel, J. and Uhl, J.J., Vector measures (Mathematical Surveys, 15. American Mathematical Society, Providence, Rhode Island, 1977).CrossRefGoogle Scholar
[11]Dinculeanu, N., Vector measures (Pergamon Press, London, 1967).CrossRefGoogle Scholar
[12]Dunford, Nelson and Schwartz, Jacob T., Linear operators. I (Interscience [John Wiley & Sons], New York, London, 1958).Google Scholar
[13]Floret, K., Weakly compact sets (Lectures Notes in Mathematics, 801. Springer-Verlag, Berlin, Heidelberg, New York, 1980).CrossRefGoogle Scholar
[14]Hermes, H., “Calculus of set valued functions”, J. Math. Mech. 18 (1968), 47–60.Google Scholar
[15]Hermes, H., “The generalized differential equation x ∈ R(t, x)”, Adv. in Math. 4 (1970), 149–169.CrossRefGoogle Scholar
[16]Hiai, F. and Umegaki, H., “Integrals, conditional expectations and martingales of multivalued functions”, J. Multivariate Anal. 7 (1977), 149–182.CrossRefGoogle Scholar
[17]Hildenbrandt, W., Core and equilibria of large economies (Princeton University Press, Princeton, New Jersey, 1974).Google Scholar
[18]Himmelberg, C.J., “Measurable relations”, Fund. Math. 87 (1975), 53–72.CrossRefGoogle Scholar
[19]Himmelberg, C.J., Parthasarathy, T. and van Vieck, F.S., “On measurable relations”, Fund. Math. 111 (1981), 161–167.CrossRefGoogle Scholar
[20]Khurana, S., “Weak sequential convergence in and Dunford-Pettis property of ”, Proc. Amer. Math. Soc. 78 (1980), 85–88.Google Scholar
[21]Mosco, U., “On the continuity of the Young-Funchel transform”, J. Math. Anal. Appl. 35 (1971), 518–535.CrossRefGoogle Scholar
[22]Papageorgiou, Nikolaos S., “Representation of set valued operators”, Trans. Amer. Math. Soc. (to appear).Google Scholar
[23]Rockafellar, R.T., “Measurable dependence of convex sets and functions in parameters”, J. Math. Anal. Appl. 28 (1969), 4–25.CrossRefGoogle Scholar
[24]Rockafellar, R.T., “Integral functionals, normal integrands and measurable selectors”, Nonlinear operators and calculus of variations, 156–209 (Lecture Notes in Mathematics, 543. Springer-Verlag, Berlin, Heidelberg, New York, 1976).Google Scholar
[25]Salinetti, G. and Wets, R., “On the relations between two types of convergence for convex functionals”, J. Math. Anal. Appl. 60 (1977), 211–226.CrossRefGoogle Scholar
[26]Salinetti, G. and Wets, R., “On the convergence of closed valued measurable multifunctions”, Trans. Amer. Math. Soc. 266 (1981), 274–289.Google Scholar
[27]Scorza-Dragoni, G., “Sulla derivazione degli integrali indefinita”, Rend. Acad. Naz. Lincei. 20 (1956), 711–714.Google Scholar