Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pastijn, F.
1991.
Commuting fully invariant congruences on free completely regular semigroups.
Transactions of the American Mathematical Society,
Vol. 323,
Issue. 1,
p.
79.
Reilly, Norman R.
and
Zhang, Shuhua
1997.
Complete endomorphisms of the lattice of pseudovarieties of finite semigroups.
Bulletin of the Australian Mathematical Society,
Vol. 55,
Issue. 2,
p.
207.
Pastijn, F.
and
Trotter, P. G.
1998.
Complete Congruences on Lattices of Varieties and of Pseudovarieties.
International Journal of Algebra and Computation,
Vol. 08,
Issue. 02,
p.
171.
Petrich, Mario
2007.
Canonical Varieties of Completely Regular Semigroups.
Journal of the Australian Mathematical Society,
Vol. 83,
Issue. 1,
p.
87.
PETRICH, MARIO
2013.
CHARACTERIZING SOME COMPLETELY REGULAR SEMIGROUPS BY THEIR SUBSEMIGROUPS.
Journal of the Australian Mathematical Society,
Vol. 94,
Issue. 3,
p.
397.
Petrich, M.
2015.
An equation for operators on varieties of completely regular semigroups.
Acta Mathematica Hungarica,
Vol. 146,
Issue. 2,
p.
341.
Petrich, Mario
2015.
New operators for varieties of completely regular semigroups.
Semigroup Forum,
Vol. 91,
Issue. 2,
p.
415.
Petrich, Mario
2015.
Varieties of completely regular semigroups related to canonical varieties.
Semigroup Forum,
Vol. 90,
Issue. 1,
p.
53.
Shaprynskiǐ, Vyacheslav Yu.
Skokov, Dmitry V.
and
Vernikov, Boris M.
2016.
Special elements of the lattice of epigroup varieties.
Algebra universalis,
Vol. 76,
Issue. 1,
p.
1.
Petrich, M.
2018.
Clusters of varieties of completely regular semigroups.
Acta Mathematica Hungarica,
Vol. 154,
Issue. 2,
p.
429.
Petrich, Mario
2018.
Ladders and canonical varieties of completely regular semigroups.
Periodica Mathematica Hungarica,
Vol. 76,
Issue. 2,
p.
133.
Petrich, Mario
2019.
A conjecture for varieties of completely regular semigroups.
Mathematica Slovaca,
Vol. 69,
Issue. 3,
p.
541.
Reilly, Norman R.
2019.
Kernel classes of varieties of completely regular semigroups II.
Semigroup Forum,
Vol. 99,
Issue. 3,
p.
840.
Reilly, Norman R.
2019.
Kernel classes of varieties of completely regular semigroups I.
Semigroup Forum,
Vol. 99,
Issue. 3,
p.
814.
Kad’ourek, Jiří
2019.
On singleton kernel classes in the lattice of varieties of completely regular semigroups.
International Journal of Algebra and Computation,
Vol. 29,
Issue. 08,
p.
1383.
Petrich, Mario
2020.
On some intervals of varieties of completely regular semigroups.
Semigroup Forum,
Vol. 100,
Issue. 2,
p.
513.
Kad’ourek, Jiří
and
Klíma, Ondřej
2021.
Libor Polák (1950–2020).
Semigroup Forum,
Vol. 102,
Issue. 2,
p.
315.
Kad’ourek, Jiří
2021.
On bases of identities of finite central locally orthodox completely regular semigroups.
Semigroup Forum,
Vol. 102,
Issue. 3,
p.
697.
Szendrei, Mária B.
and
Silva, Pedro V.
2022.
A tribute to Mario Petrich.
Semigroup Forum,
Vol. 104,
Issue. 1,
p.
1.
Gusev, Sergey V.
Lee, Edmond W. H.
and
Vernikov, Boris M.
2022.
The lattice of varieties of monoids.
Japanese Journal of Mathematics,
Vol. 17,
Issue. 2,
p.
117.


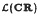 of the title then the map given by
of the title then the map given by 