Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1974.
Random Integral Equations with Applications to Life Sciences and Engineering.
Vol. 108,
Issue. ,
p.
260.


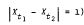 , then given any mean square continuous random function, there is a sequence in
, then given any mean square continuous random function, there is a sequence in 