Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-18T00:12:47.142Z Has data issue: false hasContentIssue false
  • English
  • Français

STOCHASTIC POTENTIALS OF INTERMITTENT MAPS

Part of: Smooth dynamical systems: general theory Low-dimensional dynamical systems Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  18 June 2020

HUAIBIN LI Open the ORCID record for HUAIBIN LI [Opens in a new window]
HUAIBIN LI*
Affiliation:
School of Mathematics and Statistics,Henan University, Kaifeng475004, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider an intermittent map 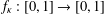$f_{\unicode[STIX]{x1D705}}:[0,1]\rightarrow [0,1]$ and a Hölder continuous potential 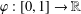$\unicode[STIX]{x1D711}:[0,1]\rightarrow \mathbb{R}$. We show that 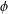$\unicode[STIX]{x1D719}$ is stochastic for 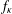$f_{\unicode[STIX]{x1D705}}$ if and only if the topological pressure 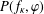$P(f_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D711})$ satisfies 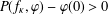$P(f_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711}(0)>0$. As a consequence, for each 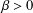$\unicode[STIX]{x1D6FD}>0$ sufficiently small, the set of Hölder continuous potentials of exponent 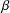$\unicode[STIX]{x1D6FD}$ that are not stochastic for 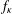$f_{\unicode[STIX]{x1D705}}$ has nonempty interior in the space of all such potentials.

Keywords

intermittent mapHölder continuous potentialstochastic potential

MSC classification

Primary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Secondary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37C40: Smooth ergodic theory, invariant measures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 145 - 153
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by the National Natural Science Foundation of China (Grant No. 11871194).

References

Aaronson, J., An Introduction to Infinite Ergodic Theory, Mathematical Surveys and Monographs, 50 (American Mathematical Society, Providence, RI, 1997).10.1090/surv/050CrossRefGoogle Scholar
Baladi, V., Positive Transfer Operators and Decay of Correlations, Advanced Series in Nonlinear Dynamics, 16 (World Scientific, River Edge, NJ, 2000).10.1142/3657CrossRefGoogle Scholar
Bowen, R., Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms, Lecture Notes in Mathematics, 470 (Springer, Berlin, 1975).10.1007/BFb0081279CrossRefGoogle Scholar
Bruin, H. and Todd, M., ‘Equilibrium states for interval maps: potentials with sup𝜙-inf𝜙 < h top(f)’, Comm. Math. Phys. 283(3) (2008), 579–611.10.1007/s00220-008-0596-0CrossRefGoogle Scholar
Bruin, H. and Todd, M., ‘Erratum to “Equilibrium states for interval maps: potentials with sup𝜙-inf𝜙 < h top(f)”’, Comm. Math. Phys. 304(2) (2011), 583–584.10.1007/s00220-011-1241-xCrossRefGoogle Scholar
Dobbs, N., ‘Measures with positive Lyapunov exponent and conformal measures in rational dynamics’, Trans. Amer. Math. Soc. 364 (2012), 2803–2824.10.1090/S0002-9947-2012-05366-9CrossRefGoogle Scholar
Keller, G., Equilibrium States in Ergodic Theory, London Mathematical Society Student Texts, 42 (Cambridge University Press, Cambridge, 1998).10.1017/CBO9781107359987CrossRefGoogle Scholar
Ledrappier, F., ‘Some properties of absolutely continuous invariant measures on an interval’, Ergod. Th. & Dynam. Sys. 1(1) (1981), 77–93.10.1017/S0143385700001176CrossRefGoogle Scholar
Li, H. and Rivera-Letelier, J., ‘Equilibrium states of interval maps for hyperbolic potentials’, Nonlinearity 27 (2014), 1779–1804.10.1088/0951-7715/27/8/1779CrossRefGoogle Scholar
Li, H. and Rivera-Letelier, J., ‘Equilibrium states of weakly hyperbolic one-dimensional maps for Hölder potentials’, Comm. Math. Phys. 328(1) (2014), 397–419.10.1007/s00220-014-1952-xCrossRefGoogle Scholar
Liverani, C., Saussol, B. and Vaienti, S., ‘Conformal measure and decay of correlation for covering weighted systems’, Ergod. Th. & Dynam. Sys. 18(6) (1998), 1399–1420.10.1017/S0143385798118023CrossRefGoogle Scholar
Pollicott, M., Sharp, R. and Yuri, M., ‘Large deviations for maps with indifferent fixed points’, Nonlinearity 11(4) (1998), 1173–1184.10.1088/0951-7715/11/4/023CrossRefGoogle Scholar
Przytycki, F., ‘On the Perron–Frobenius–Ruelle operator for rational maps on the Riemann sphere and for Hölder continuous functions’, Bol. Soc. Bras. Mat. (N.S.) 20(2) (1990), 95–125.10.1007/BF02585438CrossRefGoogle Scholar
Przytycki, F. and Urbański, M., Conformal Fractals: Ergodic Theory Methods, London Mathematical Society Lecture Note Series, 371 (Cambridge University Press, Cambridge, 2010).10.1017/CBO9781139193184CrossRefGoogle Scholar
Rivera-Letelier, J., ‘On the asymptotic expansion of maps with disconnected Julia set’, Preprint, 2012, arXiv:1206.2376v1.Google Scholar
Ruelle, D., ‘A measure associated with axiom-A attractors’, Amer. J. Math. 98(3) (1976), 619–654.10.2307/2373810CrossRefGoogle Scholar
Ruelle, D., Dynamical Zeta Functions for Piecewise Monotone Maps of the Interval, CRM Monograph Series, 4 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Sarig, O. M., ‘Phase transitions for countable Markov shifts’, Comm. Math. Phys. 217(3) (2001), 555–577.10.1007/s002200100367CrossRefGoogle Scholar
Sinaĭ, J. G., ‘Gibbs measures in ergodic theory’, Uspekhi Mat. Nauk 27(4(166)) (1972), 21–64.Google Scholar
Sullivan, D., ‘Conformal dynamical systems’, in: Geometric Dynamics, Rio de Janeiro, 1981, Lecture Notes in Mathematics, 1007 (Springer, Berlin, 1983), 725–752.Google Scholar
Zweimüller, R., ‘Invariant measures for general(ized) induced transformations’, Proc. Amer. Math. Soc. 133(8) (2005), 2283–2295.10.1090/S0002-9939-05-07772-5CrossRefGoogle Scholar