Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T03:07:30.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Some symmetric varieties of groups

Published online by Cambridge University Press:  17 April 2009

Narain Gupta  and
Frank Levin
Narain Gupta
Affiliation:
University of Manitoba, Winnipeg, Canada
Frank Levin
Affiliation:
Rutgers, The State University, New Brunswick, New Jersey, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 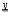(n, σ, d) denote the variety of all groups defined by the left-normed commutator identity [x1, …, xn] = [x1σ, …, xnσ]d, where σ is a non-identity permutation of {1, …, n}, and d is an integer, possibly negative. It is shown that 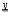(n, σ, d) is nilpotent-by-nilpotent if σ ≠ (1, 2), abelian by nilpotent if n > 2, nσ ≠ n, and nilpotent of class at most n + 1 if {1, 2} ≠ {1σ, 2σ}. This improves on a result of E.B. Kikodze that 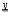(n, σ, 1) is locally soluble and if {1, 2} ≠ {1σ, 2σ} is locally nilpotent.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 3 , Issue 1 , August 1970 , pp. 97 - 105
Copyright
Copyright © Australian Mathematical Society 1970

References

[1] Gupta, N.D., “Certain locally metanilpotent varieties of groups”, Arch. Math. 20 (1969), 481–484).Google Scholar
[2] Kikodze, E.B., “Some identities in groups” (English), Math. USSR -Izvestija 1 (1967), 253–258.Google Scholar
[3] Levi, F.W., “Groups in which the commutator relation satisfies certain algebraic conditions”, J. Indian Math. Soc. (N.S.) 6 (1942), 87–97.Google Scholar
[4] Levin, Frank, “On some varieties of soluble groups. II”, Math. Z. 103 (1968), 162–172.Google Scholar
[5] Macdonald, I.D., “On certain varieties of groups”, Math. Z. 76 (1961), 270–282.CrossRefGoogle Scholar
[6] Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37, Springer-Verlag, Berlin, Heidelberg, New York, 1967).Google Scholar