Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T02:12:38.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Some properties of the projective tensor product U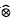X derived from those of U and X

Published online by Cambridge University Press:  17 April 2009

Patrick N. Dowling
Patrick N. Dowling
Affiliation:
Department of Mathematics and Statistics, Miami University, Oxford, OH 45056, United States of America, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a real or complex Banach space and let U be a Banach space with an unconditional basis. We show that the projective tensor product of U and X, U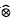X, has the complete continuity property (respectively, the analytic complete continuity property) whenever U and X have the complete continuity property (respectively, the analytic complete continuity property). More general versions of these results are also obtained. Moreover, the techniques applied here to the projective tensor product, can also be used to establish some Banach space properties of the Fremlin projective tensor product.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 1 , February 2006 , pp. 37 - 45
Copyright
Copyright © Australian Mathematical Society 2006

References

Referenes

[1]Bourgain, J. and Pisier, G., ‘A construction of L ∞-spaces and related Banach spaces’, Bol. Soc. Brasil. Mat. 14 (1983), 109–123.CrossRefGoogle Scholar
[2]Bourgain, J. and Rosenthal, H.P., ‘Applications of the theory of semi-embeddings to Banach space theory’, J. Funct. Anal. 52 (1983), 149–188.CrossRefGoogle Scholar
[3]Bu, Q., ‘Observations about the projective tensor product of Banach spaces, II — LP (0, 1)⊗⌢X, 1 < p < ∞’, Quaestiones Math. 25 (2002), 209–227.CrossRefGoogle Scholar
[4]Bu, Q. and Buskes, G., ‘The Radon-Nikodym property for tensor products of Banach lattices’, Positivity (to appear).Google Scholar
[5]Bu, Q. and Diestel, J., ‘Observations about the projective tensor product of Banach spaces, I — ℓp⊗⌢X, 1 < p < ∞’, Quaestiones Math 24 (2001), 519–533.CrossRefGoogle Scholar
[6]Bu, Q., Diestel, J., Dowling, P.N. and Oja, E., ‘Types of Radon-Nikodym properties for the projective tensor product of Banach spaces’, Illinois J. Math. 47 (2003), 1303–1326.CrossRefGoogle Scholar
[7]Bu, Q. and Dowling, P.N., ‘Observations about the projective tensor product of Banach spaces, III — Lp[0, 1] ⊗⌢X, 1 < p < ∞’, Quaestiones Math. 25 (2002), 303–310.CrossRefGoogle Scholar
[8]Bukhvalov, A.V., ‘Geometric properties of Banach spaces of measurable vector-valued functions’, Dokl. Akad. Nauk SSSR 239 (1978), 1279–1282.Google Scholar
[9]Costé, A. and Lust-Piquard, F., ‘Opérateurs sur un espace L 1’, Colloq. Math. 51 (1987), 43–66.CrossRefGoogle Scholar
[10]Diestel, J. and Uhl, J.J. Jr., Vector measures, Math. Surveys 15 (American Mathematical Society, Providence, R.I., 1977).CrossRefGoogle Scholar
[11]Dowling, P.N., ‘Radon-Nikodým properties associated with subsets of countable discrete abelian groups’, Trans. Amer. Math. Soc. 327 (1991), 879–890.Google Scholar
[12]Dowling, P.N., ‘Duality in some vector-valued function spaces’, Rocky Mountain J. Math. 22 (1992), 511–518.CrossRefGoogle Scholar
[13]Dowling, P.N., ‘Stability of Banach space properties in the projective tensor product’, Quaestiones Math. 27 (2004), 1–7.CrossRefGoogle Scholar
[14]Edgar, G.A., ‘Banach spaces with the analytic Radon-Nikodým property and compact abelian groups’, in Almost everywhere convergence (Columbus, OH, 1988) (Academic Press, Boston, MA, 1989), pp. 195–213.Google Scholar
[15]Fremlin, D.H., ‘Tensor products of Archimedean vector lattices’, Amer. J. Math. 94 (1972), 778–798.CrossRefGoogle Scholar
[16]Fremlin, D.H., ‘Tensor products of Banach lattices’, Math. Ann. 211 (1974), 87–106.CrossRefGoogle Scholar
[17]Freniche, F., García-Vázquez, J and Rodríguez-Piazza, L., ‘Tensor products and operators in spaces of analytic functions’, J. London Math. Soc. (2) 63 (2001), 705–720.CrossRefGoogle Scholar
[18]Ghoussoub, N. and Saab, E., ‘On the weak Radon-Nikodým property’, Proc. Amer. Math. Soc. 81 (1981), 81–84.Google Scholar
[19]Hensgen, W., ‘Some properties of the vector-valued Banach ideal space E(X) derived from those of E and X’, Collect. Math. 43 (1992), 1–13.Google Scholar
[20]Kaufman, R., Petrakis, M., Riddle, L. and Uhl, J.J. Jr., ‘Nearly representable operators’, Trans. Amer. Math. Soc. 312 (1989), 315–333.CrossRefGoogle Scholar
[21]Kwapień, S., ‘On Banach spaces containing c 0’, A supplement to the paper by J. Hoffmann-Jφrgensen: “Sums of independent Banach space valued random variables”, Studia Math. 52 (1974), 159–186 and 187–188.Google Scholar
[22]Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II, function spaces (Springer-Verlag, Berlin, Heidelberg, New York, 1979).CrossRefGoogle Scholar
[23]Pisier, G., ‘Une propriété de stabilité de la classe des espaces ne contenant pas l 1’, C. R. Acad. Sci. Paris Sér. A 286 (1978), 747–749.Google Scholar
[24]Randrianantoanina, N., ‘Banach spaces with complete continuity properties’, Quaestiones Math. 25 (2002), 29–36.CrossRefGoogle Scholar
[25]Randrianantoanina, N. and Saab, E., ‘The complete continuity property in Bochner function spaces’, Proc. Amer. Math. Soc. 117 (1993), 1109–1114.CrossRefGoogle Scholar
[26]Randrianantoanina, N. and Saab, E., ‘Stability of some types of Radon-Nikodým properties’, Illinois J. Math. 39 (1995), 416–430.CrossRefGoogle Scholar
[27]Randrianantoanina, N. and Saab, E., ‘The near Radon-Nikodým property in Lebesgue-Bochner function spaces’, Illinois J. Math. 42 (1998), 40–57.CrossRefGoogle Scholar
[28]Robdera, M. and Saab, P., ‘The analytic complete continuity property’, J. Math. Anal. Appl. 252 (2000), 967–979.CrossRefGoogle Scholar
[29]Robdera, M. and Saab, P., ‘Complete continuity properties of Banach spaces associated with subsets of a discrete abelian group’, Glasgow Math. J. 43 (2001), 185–198.CrossRefGoogle Scholar
[30]Rudin, W., Fourier analysis on groups (Interscience Publishers, New York, London, 1962).Google Scholar
[31]Turett, B. and Uhl, J.J. Jr., ‘Lp(μ, X) (1 < p < ∞) has the Radon-Nikodým property if X does by martingales’, Proc. Amer. Math. Soc. 61 (1976), 347–350.Google Scholar