Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kovács, L. G.
and
Newman, M. F.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
417.
Bryce, R. A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
150.
Bryce, R. A.
and
Cossey, John
1974.
Metanilpotent fitting classes.
Journal of the Australian Mathematical Society,
Vol. 17,
Issue. 3,
p.
285.
Kovács, L. G.
and
Newman, M. F.
1974.
Proceedings of the Second International Conference on The Theory of Groups.
Vol. 372,
Issue. ,
p.
417.
Bryce, R. A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
150.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.


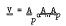 with
with 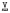 distributive and has descending chain condition and that
distributive and has descending chain condition and that 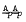 is its only just non-Cross subvariety. When
is its only just non-Cross subvariety. When 