Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-10T12:49:30.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Some extensions of additive properties of general sequences

Published online by Cambridge University Press:  17 April 2009

Min Tang
Min Tang
Affiliation:
Department of Mathematics, Anhui Normal University, Wuhu 241000, China Department of Mathematics, Nanjing Normal University, Nanjing 210097, China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A = {a1, a2,…}(a1 < a2 < …) be an infinite sequence of positive integers. Let k ≥ 2 be a fixed integer and denote by Rk(n) the number of solutions of 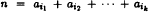. Erdős, Sárközy and Sós studied the boundness of |R2(n + 1) − R2(n)| and the monotonicity property of R2(n). In this paper, we extend some results to k > 2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 1 , February 2006 , pp. 139 - 146
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.CrossRefGoogle Scholar
[2]Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, I’, Pacific J. Math. 118 (1985), 347–357.Google Scholar
[3]Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, II’, Acta Math. Hungar. 48 (1986), 201–211.Google Scholar
[4]Erdős, P., Sárközy, A. and Sós, V.T., ‘Problems and results on additive properties of general sequences, III’, Studia Sci. Math. Hungar. 22 (1987), 53–63.Google Scholar
[5]Erdős, P., Sárközy, A. and Sós, V.T., ‘Problems and results on additive properties of general sequences, IV’, in in: Number theory (Ootacamund, 1984), Lecture Notes in Math. 1122 (Springer-Verlag, Berlin, 1985), pp. 85–104.Google Scholar
[6]Horváth, G., ‘On an additive property of sequences of nonnegative integers’, Period. Math. Hungar. 45 (2002), 73–80.Google Scholar