Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T19:36:34.169Z Has data issue: false hasContentIssue false
  • English
  • Français

REMARKS ON THE MIXED JOINT UNIVERSALITY FOR A CLASS OF ZETA FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  19 October 2016

ROMA KAČINSKAITĖ  and
KOHJI MATSUMOTO
ROMA KAČINSKAITĖ
Affiliation:
Department of Mathematics, Šiauliai University, Višinskio 19, LT-77156 Šiauliai, Lithuania Department of Mathematics and Statistics, Vytautas Magnus University, Kaunas, Vileikos 8, LT-44404, Lithuania email [email protected], [email protected]
KOHJI MATSUMOTO*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

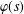Two results related to the mixed joint universality for a polynomial Euler product $\unicode[STIX]{x1D711}(s)$ and a periodic Hurwitz zeta function 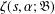$\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D6FC};\mathfrak{B})$, when $\unicode[STIX]{x1D6FC}$ is a transcendental parameter, are given. One is the mixed joint functional independence and the other is a generalised universality, which includes several periodic Hurwitz zeta functions.

Keywords

functional independenceperiodic Hurwitz zeta functionpolynomial Euler productuniversality

MSC classification

Primary: 11M35: Hurwitz and Lerch zeta functions
Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 187 - 198
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Genys, J., Macaitienė, R., Račkauskienė, S. and Šiaučiūnas, D., ‘A mixed joint universality theorem for zeta-functions’, Math. Model. Anal. 15(4) (2010), 431–446.Google Scholar
Hilbert, D., ‘Mathematische Probleme’, Nachr. Königl. Ges. Wiss. Göttingen Math.-Phys. Kl. 7 (1900), 253–297; also in D. Hilbert, Gesammelte Abhandlungen, Vol. III (Chelsea, New York, 1965) (originally 1935), 290–329.Google Scholar
Javtokas, A. and Laurinčikas, A., ‘On the periodic Hurwitz zeta-function’, Hardy–Ramanujan J. 29 (2006), 18–36.Google Scholar
Kačinskaitė, R. and Laurinčikas, A., ‘The joint distribution of periodic zeta-functions’, Studia Sci. Math. Hungar. 48 (2011), 257–279.Google Scholar
Kačinskaitė, R. and Matsumoto, K., ‘The mixed joint universality for a class of zeta-functions’, Math. Nachr. 288 (2015), 1900–1909.Google Scholar
Laurinčikas, A., Limit Theorems for the Riemann Zeta-Function (Kluwer Academic, Dordrecht, 1996).Google Scholar
Laurinčikas, A., ‘Functional independence of periodic Hurwitz zeta-functions’, Mat. Zametki 81(1) (2008), 69–78 (in Russian); Math. Notes 83(1) (2008), 65–71.Google Scholar
Laurinčikas, A. and Šiaučiūnas, D., ‘A mixed joint universality theorem for zeta-functions’, in: Analytic and Probabilistic Methods in Number Theory, J. Kubilius Memorial Volume (eds. Laurinčikas, A. et al. ) (TEV, Vilnius, 2012), 185–195.Google Scholar
Laurinčikas, A. and Skerstonaitė, S., ‘A joint universality theorem for periodic Hurwitz zeta-functions’, Lith. Math. J. 49 (2009), 287–296.Google Scholar
Laurinčikas, A. and Skerstonaitė, S., ‘Joint universality for periodic Hurwitz zeta-functions II’, in: New Directions in Value-Distribution Theory of Zeta and L-Functions (eds. Steuding, R. and Steuding, J.) (Shaker, Aachen, 2009), 161–169.Google Scholar
Matsumoto, K., ‘Value-distribution of zeta-functions’, in: Analytic Number Theory, Proc. Japanese–French Sympos., Tokyo, Lecture Notes in Mathematics, 1434 (eds. Nagasaka, K. and Fouvry, E.) (Springer, Berlin, 1990), 178–187.Google Scholar
Mishou, H., ‘The joint value distribution of the Riemann zeta function and Hurwitz zeta-function’, Lith. Math. J. 47 (2007), 32–47.Google Scholar
Pocevičienė, V. and Šiaučiūnas, D., ‘A mixed joint universality theorem for zeta-functions. II’, Math. Model. Anal. 19 (2014), 52–65.Google Scholar
Steuding, J., Value-Distribution of $L$ -Functions and Allied Zeta Functions – with an Emphasis on Aspects of Universality, Habilitationschrift (J.W. Goethe University, Frankfurt, 2003).Google Scholar
Steuding, J., Value-Distribution of L-Functions, Lecture Notes in Mathematics, 1877 (Springer, Berlin, 2007).Google Scholar
Voronin, S. M., ‘On the functional independence of 𝜁-functions’, Sov. Math. Dokl. 14 (1973), 607–609 (in Russian); Dokl. Akad. Nauk SSSR 209 (1973), 1264–1266.Google Scholar
Voronin, S. M., Analytic Properties of Generating Dirichlet Functions of Arithmetical Objects, PhD Thesis (Moscow, 1977) (in Russian).Google Scholar