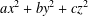Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-16T15:51:23.524Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIME-UNIVERSAL QUADRATIC FORMS $ax^{2}+by^{2}+cz^{2}$ AND 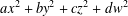$ax^{2}+by^{2}+cz^{2}+dw^{2}$

Part of: Elementary number theory Forms and linear algebraic groups

Published online by Cambridge University Press:  27 September 2019

GREG DOYLE Open the ORCID record for GREG DOYLE [Opens in a new window]  and
KENNETH S. WILLIAMS Open the ORCID record for KENNETH S. WILLIAMS [Opens in a new window]
GREG DOYLE
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON K1S 5B6, Canada email [email protected]
KENNETH S. WILLIAMS*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON K1S 5B6, Canada email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A positive-definite diagonal quadratic form 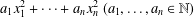$a_{1}x_{1}^{2}+\cdots +a_{n}x_{n}^{2}\;(a_{1},\ldots ,a_{n}\in \mathbb{N})$ is said to be prime-universal if it is not universal and for every prime 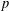$p$ there are integers 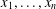$x_{1},\ldots ,x_{n}$ such that 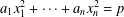$a_{1}x_{1}^{2}+\cdots +a_{n}x_{n}^{2}=p$. We determine all possible prime-universal ternary quadratic forms 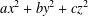$ax^{2}+by^{2}+cz^{2}$ and all possible prime-universal quaternary quadratic forms 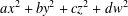$ax^{2}+by^{2}+cz^{2}+dw^{2}$. The prime-universal ternary forms are completely determined. The prime-universal quaternary forms are determined subject to the validity of two conjectures. We make no use of a result of Bhargava concerning quadratic forms representing primes which is stated but not proved in the literature.

Keywords

ternary quadratic formsquaternary quadratic formsprime-universality

MSC classification

Primary: 11E20: General ternary and quaternary quadratic forms; forms of more than two variables
Secondary: 11A41: Primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 1 - 12
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Bhargava, M., ‘On the Conway–Schneeberger fifteen theorem’, in: Quadratic Forms and their Applications, Dublin 1999, Contemporary Mathematics, 272 (American Mathematical Society, Providence, RI, 2000), 27–37.Google Scholar
Dickson, L. E., Modern Elementary Theory of Numbers (University of Chicago Press, Chicago, 1947).Google Scholar
Duke, W., ‘On ternary quadratic forms’, J. Number Theory 110 (2005), 37–43.Google Scholar
Earnest, A. G. and Haensch, A., ‘Completeness of the list of spinor regular ternary quadratic forms’, Mathematika 65 (2019), 213–235.Google Scholar
Hahn, A. J., ‘Quadratic forms over ℤ from Diophantus to the 290 theorem’, Adv. Appl. Clifford Algebr. 18 (2008), 665–676.Google Scholar
Kaplansky, I., ‘Ternary positive quadratic forms that represent all odd positive integers’, Acta Arith. 70 (1995), 209–214.Google Scholar
Kim, B. M., Kim, M.-H. and Oh, B.-K., ‘A finiteness theorem for representability of integral quadratic forms by forms’, J. reine angew. Math. 581 (2005), 23–30.Google Scholar
Kim, M.-H., ‘Recent developments on universal forms’, in: Algebraic and Arithmetic Theory of Quadratic Forms, Contemporary Mathematics, 344 (American Mathematical Society, Providence, RI, 2004), 215–228.Google Scholar
Ono, K. and Soundararajan, K., ‘Ramanujan’s ternary quadratic form’, Invent. Math. 130(3) (1997), 415–454.Google Scholar
Ramanujan, S., ‘On the expression of a number in the form ax 2 + by 2 + cz 2 + du 2 ’, Trans. Camb. Philos. Soc. 22(9) (1916), 11–21.Google Scholar
Rouse, J., ‘Quadratic forms representing all odd positive integers’, Amer. J. Math. 136(6) (2014), 1693–1745.Google Scholar
Williams, K. S., ‘A “Four Integers” theorem and a “Five Integers” theorem’, Amer. Math. Monthly 122 (2015), 528–536.Google Scholar