No CrossRef data available.
Article contents
POSITIVE PERIODIC SOLUTIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS WITH SINGULARITIES
Part of:
Boundary value problems
Published online by Cambridge University Press: 01 August 2008
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this work, we consider the periodic boundary value problem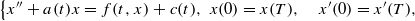 
where a,c∈L1(0,T) and f is a Carathéodory function. An existence theorem for positive periodic solutions is proved in the case where the associated Green function is nonnegative. Our result is valid for systems with strong singularities, and answers partially the open problem raised in Torres [‘Weak singularities may help periodic solutions to exist’, J. Differential Equations232 (2007), 277–284].
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2008 Australian Mathematical Society
References
[1]Bonheure, D., Fabry, C. and Smets, D., ‘Periodic solutions of forced isochronous oscillators at resonance’, Discrete Contin. Dyn. Syst. 8 (2002), 907–930.CrossRefGoogle Scholar
[2]Chu, J., Torres, P. J. and Zhang, M., ‘Periodic solutions of second order non-autonomous singular dynamical systems’, J. Differential Equations 239(1) (2007), 196–212.CrossRefGoogle Scholar
[3]Fonda, A., Manásevich, R. and Zanolin, F., ‘Subharmonic solutions for some second order differential equations with singularities’, SIAM J. Math. Anal. 24 (1993), 1294–1311.CrossRefGoogle Scholar
[4]Habets, P. and Sanchez, L., ‘Periodic solutions of some Linard equations with singularities’, Proc. Amer. Math. Soc. 109 (1990), 1135–1144.Google Scholar
[5]Jiang, D., Chu, J. and Zhang, M., ‘Multiplicity of positive periodic solutions to superlinear repulsive singular equations’, J. Differential Equations 211(2) (2005), 282–302.CrossRefGoogle Scholar
[6]Lazer, A. C. and Solimini, S., ‘On periodic solutions of nonlinear differential equations with singularities’, Proc. Amer. Math. Soc. 99 (1987), 109–114.CrossRefGoogle Scholar
[7]del Pino, M. and Manásevich, R., ‘Infinitely many T-periodic solutions for a problem arising in nonlinear elasticity’, J. Differential Equations 103 (1993), 260–277.CrossRefGoogle Scholar
[8]Rachunková, I., Stanek, S. and Tvrdý, M., Singularities and Laplacians in Boundary Value Problems for Nonlinear Ordinary Differential Equations, Handbook of Differential Equations (Ordinary Differential Equations), 3 (Elsevier, Amsterdam, 2006).CrossRefGoogle Scholar
[9]Rachunková, I., Tvrdý, M. and Vrkoc˘, I., ‘Existence of nonnegative and nonpositive solutions for second order periodic boundary value problems’, J. Differential Equations 176 (2001), 445–469.CrossRefGoogle Scholar
[10]Ramos, M. and Terracini, S., ‘Noncollision periodic solutions to some singular dynamical systems with very weak forces’, J. Differential Equations 118 (1995), 121–152.CrossRefGoogle Scholar
[11]Torres, P. J., ‘Existence of one-signed periodic solutions of some second order differential equations via a Krasnoselskii fixed point theorem’, J. Differential Equations 190 (2003), 643–662.CrossRefGoogle Scholar
[12]Torres, P. J., ‘Weak singularities may help periodic solutions to exist’, J. Differential Equations 232 (2007), 277–284.CrossRefGoogle Scholar
[13]Torres, P. J. and Zhang, M., ‘Twist periodic solutions of repulsive singular equations’, Nonlinear Anal. 56 (2004), 591–599.CrossRefGoogle Scholar
[14]Zhang, M., ‘A relationship between the periodic and the Dirichlet BVPs of singular differential equations’, Proc. Roy. Soc. Edinburgh Sect. A 128 (1998), 1099–1114.CrossRefGoogle Scholar
You have
Access