Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T14:59:14.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation criteria for certain second order nonlinear difference equations

Published online by Cambridge University Press:  17 April 2009

S.R. Grace  and
H.A. El-Morshedy
S.R. Grace
Affiliation:
Department of Engineering MathematicsFaculty of EngineeringCairo UniversityOrmanGiza 1200Egypt
H.A. El-Morshedy
Affiliation:
Department of Mathematics and StatisticsThe Flinders University of South AustraliaGPO Box 2100Adelaide SA 5001Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with nonlinear difference equations of the form

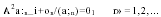
where δ is the forward difference operator defined by δun−1 = un − un −1 δ2un −1= δ(δun-1) and {an} is a real sequence which is not assumed to be nonnegative. The function f is such that uf(u) < 0 for all u ≠ 0 and f(u) − f(v) = g(u, v)(u − v), for all u, v ≠ 0, and for some nonnegative function g. Our results are not only new but also improve and generalise some recent oscillation criteria. Examples illustrating the importance of our main results are also given.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 60 , Issue 1 , August 1999 , pp. 95 - 108
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Atkinson, F.V., ‘On second order nonlinear oscillations’, Pacific J. Math. 5 (1955), 643–647.CrossRefGoogle Scholar
[2]Erbe, L., ‘Oscillation theorems for second order nonlinear differential equations’, Proc. Amer. Math. Soc. 24 (1970), 811–814.Google Scholar
[3]Grace, S.R., Abadeer, A.A. and El-Morshedy, H.A., ‘On the oscillation of certain second order difference equations’, Comm. Appl. Anal. 2 (1998), 447–456.Google Scholar
[4]Graef, J.R., Rankin, S.M. and Spikes, P.W., ‘Oscillation theorems for perturbed nonlinear differential equations’, J. Math. Anal. Appl. 65 (1978), 375–390.CrossRefGoogle Scholar
[5]Hooker, J.W. and Patula, W.T., ‘A second-order nonlinear difference equation: Oscillation and asymptotic behaviour’, J. Math. Anal. Appl. 91 (1983), 9–29.CrossRefGoogle Scholar
[6]Kiguradze, I.T., ‘A note on the oscillation of solutions of equation u′ + a(t)|u|n sgn u = 0’, (In Russian), Časopis Pěst. Mat. 92 (1967), 343–350.CrossRefGoogle Scholar
[7]Kwong, M.K. and Wong, J.S.W., ‘Linearization of second order nonlinear oscillation theorems’, Trans. Amer. Math. Soc. 279 (1983), 705–722.CrossRefGoogle Scholar
[8]Mickens, R.E., Difference equations, theory and applications (Van Nostrand, Rheinhold, New York, 1990).Google Scholar
[9]Onose, H., ‘On oscillations of nonlinear second order equations’, J. Math. Anal. Appl. 39 (1972), 122–124.CrossRefGoogle Scholar
[10]Onose, H., ‘Oscillation criteria for second order nonlinear differential equations’, Proc. Amer. Math. Soc. 51 (1975), 67–73.CrossRefGoogle Scholar
[11]Szmanda, B., ‘Oscillation of solutions of second order difference equations’, Portugal. Math. 37 (1978), 251–254.Google Scholar
[12]Thandapani, E., ‘Oscillatory behaviour of solutions of second order nonlinear difference equations’, J. Math. Phys. Sci. 25 (1991), 457–464.Google Scholar
[13]Thandapani, E., Györi, I. and Lalli, B.S., ‘An application of discrete inequality to second order nonlinear oscillation’, J. Math. Anal. Appl. 186 (1994), 200–208.CrossRefGoogle Scholar
[14]Zhang, B.G., ‘Oscillation and asymptotic behaviour of second order difference equations’, J. Math. Anal. Appl. 173 (1993), 58–68.CrossRefGoogle Scholar
[15]Zhang, B.G. and Chen, G.D., ‘Oscillation of certain second order nonlinear difference equations’, J. Math. Anal. Appl. 199 (1996), 827–841.CrossRefGoogle Scholar