Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T05:13:08.829Z Has data issue: false hasContentIssue false
  • English
  • Français

On the laws of certain varieties of groups

Published online by Cambridge University Press:  17 April 2009

Robert B. Howlett  and
Richard Levingston
Robert B. Howlett
Affiliation:
Department of Pure Mathematics, University of Sydney, Sydney, New South Wales 2006, Australia;
Richard Levingston
Affiliation:
22 Swinden Street, Downer, ACT 2602, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let m and n be coprime positive integers. The variety 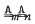(consisting of all groups G such that for some normal subgroup H of G, H is abelian of exponent dividing m and G/H is abelian of exponent dividing n) and the variety 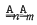both satisfy the following three laws:

all elements have order dividing mn;

the commutator of two mth powers has order dividing m;

the commutator of two nth powers has order dividing n.

It is proved that any law which holds in both these varieties (notably that commutators commute) is a consequence of the above three laws.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 31 , Issue 1 , February 1985 , pp. 145 - 154
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Richard, Levingston, “The laws of some metabelian varieties”, J. Austral. Math. Soc. Ser. A 30 (1981), 469–472.Google Scholar
[2]Hanna, Neumann, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 37. Springer-verlag, Berlin, Heidelberg, New York, 1967).Google Scholar