Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T11:27:42.277Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hölder semi-norm of the remainder in polynomial approximation

Published online by Cambridge University Press:  17 April 2009

David Elliott
David Elliott
Affiliation:
Department of MathematicsUniversity of TasmaniaGPO Box 252C Hobart Tas 7001Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose the qth derivative of a function f is Hölder continuous of index α, where 0 < α ≤ 1, on the interval [-1,1]. Suppose further that pn is any polynomial of degree at most n such that |τn(x)| = |f(x) - pn(x)| ≤ c {max ((1 - x2)½/n, 1/n2) } q+a [-1,1]. If

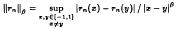
then it is shown that

‖τn‖β ≤ cn−q−α+β, 0 < β ≤ 1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 49 , Issue 3 , June 1994 , pp. 421 - 426
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Davydov, O.V., ‘Note on the approximation of functions in Lipschitz spaces’, in Approximation of functions and summation of series, (Motornyi, V.P., Editor) (DSU, Dnepropetrovsk, 1993), pp. 42–49.Google Scholar
[2]Elliott, D. and Paget, D.F., ‘Gauss type quadrature rules for Cauchy principal value integrals’, Math. Comp. 33 (1979), 301–309.CrossRefGoogle Scholar
[3]Elliott, D., ‘A comprehensive approach to the approximate solution of singular integral equations over the arc (-1,1)’, J. Integral Equations Appl. 2 (1989), 59–94.CrossRefGoogle Scholar
[4]Grünwald, G., ‘On a convergence theorem for the Lagrangian interpolation polynomials’, Bull. Amer. Math. Soc. 47 (1941), 271–275.CrossRefGoogle Scholar
[5]Ioakimidis, N.I., ‘An improvement of Kalandiya's theorem’, J. Approx. Theory 38 (1983), 354–356.CrossRefGoogle Scholar
[6]Kalandiya, A.I., ‘On a direct method of solution of an equation in wing theory with an application to the theory of elasticity’, (in Russian), Mat. Sb. 42 (1957), 249–272.Google Scholar
[7]Lorentz, G.G., Approximation of functions (Holt, Rinehart and Winston, New York, 1966).Google Scholar
[8]Mills, T.M. and Varma, A.K., ‘A new proof of A.F. Timan's approximation theorem’, Israel J. Math. 18 (1974), 39–44.CrossRefGoogle Scholar
[9]Nikolskii, S.M., ‘On the best approximation of functions satisfying Lipschitz's conditions by polynomials’, (in Russian), Izv. Akad. Nauk. SSSR Ser. Mat. 10 (1946), 295–322.Google Scholar
[10]Nikolskii, S.M., ‘A generalization of an inequality of S.N. Bernstein’, (in Russian), Dokl. Akad. Nauk. SSSR 60 (1948), 1507–1510.Google Scholar
[11]Riesz, M., ‘Les fonctions conjuguées et les séries de Fourier’, C.R. Acad. Sci. 178 (1924), 1464–1476.Google Scholar
[12]Timan, A.F., ‘A strengthening of Jackson's theorem on the best approximation of continuous functions by a polynomial on a finite segment of the real axis’, (in Russian), Dokl. Akad. Nauk SSSR 78 (1951), 17–20.Google Scholar