No CrossRef data available.
Published online by Cambridge University Press: 17 April 2009
Let S be a Hausdorff topological semigroup and Cb,(S), Cc (S), the spaces of real valued continuous functions on S which are respectively bounded and have compact support. A regular measure m on S is r*-invarient if m(B) = 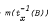 for every Borel B ⊂ S and every x ∈ S, where tx: s → sx is the right translation by x. The following theorem is proved: Let S be locally compact metric with the tx's closed. Then the following statements are equivalent: (i) S admits a right invariant integral on Cc (S). (ii) S admits an r*–invariant measure, (iii) S has a unique minimal left ideal. The above equivalence is considered also for normal semigroups and analogous results are obtained for finitely additive r*–invariant measures. Also in the case when S is a complete separable metric semigroup with the tx's closed, the following statements are equivalent: (i) S admits a right invariant integral I on Cb(S) such that I(1) = 1 and satisfying Daniel's condition. (ii) S admits an r*–invariant probability measure. (iii) S has a right ideal which is a compact group and which is contained in a unique minimal left ideal. Finally, in order that a locally compact S admit a right invariant measure, it suffices that S contain a right ideal F which is a left group such that (B ∩ F)x = BX ∩ Fx for all Borel B ⊂ S.
for every Borel B ⊂ S and every x ∈ S, where tx: s → sx is the right translation by x. The following theorem is proved: Let S be locally compact metric with the tx's closed. Then the following statements are equivalent: (i) S admits a right invariant integral on Cc (S). (ii) S admits an r*–invariant measure, (iii) S has a unique minimal left ideal. The above equivalence is considered also for normal semigroups and analogous results are obtained for finitely additive r*–invariant measures. Also in the case when S is a complete separable metric semigroup with the tx's closed, the following statements are equivalent: (i) S admits a right invariant integral I on Cb(S) such that I(1) = 1 and satisfying Daniel's condition. (ii) S admits an r*–invariant probability measure. (iii) S has a right ideal which is a compact group and which is contained in a unique minimal left ideal. Finally, in order that a locally compact S admit a right invariant measure, it suffices that S contain a right ideal F which is a left group such that (B ∩ F)x = BX ∩ Fx for all Borel B ⊂ S.