Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-02T04:51:53.623Z Has data issue: false hasContentIssue false
  • English
  • Français

On the dynamics of a periodic delay logistic equation with diffusion

Published online by Cambridge University Press:  17 April 2009

K. Gopalasamy  and
Pei-Xuan Weng
K. Gopalasamy
Affiliation:
School of Information Science and Technology Flinders University, G.P.O Box 2100 Adelaide SA 5001, Australia
Pei-Xuan Weng
Affiliation:
Department of Mathematics, South China Normal University, Guangzhou Peoples, Republic of China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Sufficient conditions are obtained for the existence of a globally attractive positive periodic solution of the periodic diffusive delay logistic system

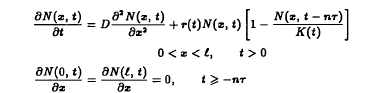
in which τ and K are positive periodic functions of period τ, n is a positive integer and ö is a nonnegative number; sufficient conditions are also obtained for all positive solutions to be oscillatory about the periodic solution.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 45 , Issue 1 , February 1992 , pp. 113 - 134
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Arnann, H., ‘Periodic solutions of semilinear parabolic equations’, in Nonlinear analysis, Editors Cesari, L., Kannan, R. and Weinberger, H.F., pp. 1–29 (Academic Press, New York, 1978).Google Scholar
[2]Barbalatt, I., ‘Systemes d'equations differentielle d'oscillations nonlineaires’, Rev. Roumaine Math. Pures Appl. 4 (1959), 267–270.Google Scholar
[3]Britton, N.F., Reaction-diffusion equations and their applications to biology (Academic Press, London, 1986).Google Scholar
[4]Cohen, D.S. and Rosenblatt, S., ‘Multispecies interactions with hereditary effects and spatial diffusion’, J. Math. Biol. 7 (1979), 231–241.Google Scholar
[5]Coleman, B.D., ‘Nonautonomous logistic equations as model of the adjustment of populations to environmental change’, Math. Biosci. 45 (1979), 159–173.CrossRefGoogle Scholar
[6]Coleman, B.D., ‘On optimal intrinsic growth rates for populations in periodically changing environment’, J. Math. Biol. 12 (1981), 343–354.Google Scholar
[7]Gopalsamy, K., He, Xue-zhong and Wen, Lizhi, ‘Global attractivity and oscillations in a periodic logistic integrodifferential equation’, Houston J. Math. 17 (1991), 157–177.Google Scholar
[8]Green, D. and Stech, H.W., ‘Diffusion and hereditary effects in a class of population models’, in Differential equations and applications in ecology, epidemics and population problems, Editors Busenberg, S. and Cooke, K.L., pp. 19–28 (Academic Press, New York, 1981).Google Scholar
[9]Hutchinson, G.E., ‘Circular causal systems in ecology’, Ann. New York Acad. Sci. 50 (1948), 221–246.Google Scholar
[10]Jones, G.S., ‘On the nonlinear difference differential equation f′(x) = -αf(x – 1)[1 + f (x)]‘, J. Math. Anal. Appl. 4 (1962), 440–469.CrossRefGoogle Scholar
[11]Kahane, C.S., ‘On the asymptotic behaviour of solutions of parabolic equations’, Czechoslovak Math. J. 33 (1983), 262–285.Google Scholar
[12]Kahane, C.S., ‘On the asymptotic behaviour of solutions of parabolic equations under homogeneous Neumann boundary conditions’, Funkcial. Ekvac. 32 (1989), 191–213.Google Scholar
[13]Kakutani, S. and Markus, L., ‘On the nonlinear difference differential equation y′(t) = [A - By(t – τ)]y(t)’, in Contribution to the theory of nonlinear oscillations (Princeton University Press, 1958).Google Scholar
[14]Kolesov, Ju. S., ‘Periodic solutions of quasilinear parabolic equations of second order’, Trans. Moscow Math. Soc. 21 (1970), 114–146.Google Scholar
[15]Koplatadze, R.G. and Canturija, T.A., ‘On oscillatory and monotone solutions of first order differential equations with deviating arguments’, Differentsial'nye Uravneniya 18 (1982), 1463–1465.Google Scholar
[16]Kreith, K. and Ladas, G., ‘Allowable delays for positive diffusion processes’, Hiroshima Math. J. 15 (1985), 437–443.CrossRefGoogle Scholar
[17]Leung, A.W., Systems of nonlinear partial differential equations (Kluwer Academic Publishers, Dordrecht, 1989).Google Scholar
[18]Lin, J. and Khan, P.B., ‘Phase and amplitude in delay-diffusion population models’, J. Math. Biol. 13 (1982), 383–393.Google Scholar
[19]Luckhaus, S., ‘Global boundedness for a delay differential equation’, Trans. Amer. Math. Soc. 294 (1986), 767–774.Google Scholar
[20]Memory, M.C., ‘Bifurcation and asymptotic behaviour of solutions of a delay differential equation with diffusion’, SIAM J. Appl. Math. 20 (1989), 533–546.Google Scholar
[21]Morita, Y., ‘Instability of spatially homogeneous periodic solutions to delay diffusion equations’, in Lecture Notes Numer. Appl. Anal. 6 (1983), 107–124. (Recent Topics in Nonlinear PDE, Hiroshima, 1984).Google Scholar
[22]Murray, J.D., ‘Spatial structures in predator-prey communities — a nonlinear time delay diffusion model’, Math. Biosci. 30 (1976), 73–85.Google Scholar
[23]Okubo, A., Diffusion and ecological problems: Mathematical models (Springer-Verlag, Berlin, 1980).Google Scholar
[24]Protter, M.H. and Weinberger, H.F., Maximum principles in differential equations (Prentice-Hall Englewood Cliffs, New Jersey, 1967).Google Scholar
[25]Redlinger, R., ‘On Volterra's population equation with diffusion’, SIAM J. Math. Anal. 36 (1985), 135–142.Google Scholar
[26]Schiaffino, A., ‘On a diffusion Volterra equation’, Nonlinear Anal. 3 (1979), 595–600.Google Scholar
[27]Tesei, A., ‘Stability properties of partial Volterra integrodifferential equations’, Ann. Mat. Pura Appl. 126 (1980), 103–115.Google Scholar
[28]Vejvoda, O., Partial differential equations: Time-periodic solutions (Martinus Nijhoff Publishers, The Hague, 1982).Google Scholar
[29]Wright, E.M., ‘A nonlinear difference differential equation’, J. Reine and Angew. Math. 194 (1955), 66–87.Google Scholar
[30]Yamada, Y., ‘On a certain class of semilinear Volterra diffusion equations’, J. Math. Anal. Appl. 88 (1982), 433–451.Google Scholar
[31]Yoshida, K., ‘The Hopf bifurcation and its stability for semilinear diffusion equation with time delay arising in ecology’, Hiroshima Math. J. 12 (1982), 321–348.Google Scholar
[32]Yoshida, K. and Khishimoto, K., ‘Effect of two delays on partially functional differential equations’, Kuramoto J. Sci. (Math.) 15 (1983), 91–109.Google Scholar
[33]Yoshida, K., ‘Oscillation of nonlinear parabolic equations with functional arguments’, Hiroshima Math. J. 16 (1986), 305–314.Google Scholar
[34]Zhang, B.G. and Gopalsamy, K., ‘Global attractivity and oscillations in a periodic delay-logistic equation’, J. Math. Anal. Appl. 150 (1990), 274–283.Google Scholar