Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T01:29:55.703Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DERIVATION LIE ALGEBRAS OF FEWNOMIAL SINGULARITIES

Part of: Local theory Singularities

Published online by Cambridge University Press:  03 May 2018

NAVEED HUSSAIN ,
STEPHEN S.-T. YAU  and
HUAIQING ZUO
NAVEED HUSSAIN
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, PR China email [email protected]
STEPHEN S.-T. YAU*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, PR China email [email protected]
HUAIQING ZUO
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

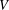Let $V$ be a hypersurface with an isolated singularity at the origin defined by the holomorphic function 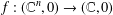$f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$. The Yau algebra, 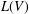$L(V)$, is the Lie algebra of derivations of the moduli algebra of $V$. It is a finite-dimensional solvable algebra and its dimension 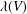$\unicode[STIX]{x1D706}(V)$ is the Yau number. Fewnomial singularities are those which can be defined by an $n$-nomial in $n$ indeterminates. Yau and Zuo [‘A sharp upper estimate conjecture for the Yau number of weighted homogeneous isolated hypersurface singularity’, Pure Appl. Math. Q.12(1) (2016), 165–181] conjectured a bound for the Yau number and proved that this conjecture holds for binomial isolated hypersurface singularities. In this paper, we verify this conjecture for weighted homogeneous fewnomial surface singularities.

Keywords

fewnomial singularityLie algebraisolated singularity

MSC classification

Primary: 14B05: Singularities
Secondary: 32S05: Local singularities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 77 - 88
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

Research partially supported by NSFC (grant nos. 11531007 and 11771231), Tsinghua University Initiative Scientific Research Program and start-up fund from Tsinghua University.

References

Arnold, V. I., Gusein-Zade, S. M. and Varchenko, A. N., Singularities of Differential Maps, Vol. 1, 2nd edn (MCNMO, Moskva, 2004).Google Scholar
Block, R., ‘Determination of the differentiably simple rings with a minimal ideal’, Ann. of Math. (2) 90 (1969), 433–459.Google Scholar
Chen, B., Chen, H., Yau, S. S.-T. and Zuo, H., ‘The non-existence of negative weight derivations on positive dimensional isolated singularities: generalized Wahl conjecture’, J. Differential Geom. to appear.Google Scholar
Ebeling, W. and Takahashi, A., ‘Strange duality of weighted homogeneous polynomials’, Compos. Math. 147 (2011), 1413–1433.CrossRefGoogle Scholar
Elashvili, A. and Khimshiashvili, G., ‘Lie algebras of simple hypersurface singularities’, J. Lie Theory 16(4) (2006), 621–649.Google Scholar
Khimshiashvili, G., ‘Yau algebras of fewnomial singularities’, Preprint, http://www.math.uu.nl/publications/preprints/1352.pdf.Google Scholar
Milnor, J. and Orlik, P., ‘Isolated singularities defined by weighted homogeneous polynomials’, Topology 9 (1970), 385–393.Google Scholar
Saeki, O., ‘Topological invariance of weights for weighted homogeneous isolated singularities in ℂ3 ’, Proc. Amer. Math. Soc. 103(3) (1988), 905–909.Google Scholar
Saito, K., ‘Quasihomogene isolierte Singularitäten von Hyperflächen’, Invent. Math. 14 (1971), 123–142.Google Scholar
Seeley, C. and Yau, S. S.-T., ‘Variation of complex structures and variation of Lie algebras’, Invent. Math. 99 (1990), 545–565.Google Scholar
Yau, S. S.-T., ‘Continuous family of finite-dimensional representations of solvable Lie algebra arising from singularities’, Proc. Natl. Acad. Sci. USA 80 (1983), 7694–7696.Google Scholar
Yau, S. S.-T., ‘Solvability of Lie algebras arising from isolated singularities and non-isolatedness of singularities defined by sl(2, C) invariant polynomials’, Amer. J. Math. 113 (1991), 773–778.CrossRefGoogle Scholar
Yau, S. S.-T. and Zuo, H., ‘Derivations of the moduli algebras of weighted homogeneous hypersurface singularities’, J. Algebra 457 (2016), 18–25.Google Scholar
Yau, S. S.-T. and Zuo, H., ‘A sharp upper estimate conjecture for the Yau number of weighted homogeneous isolated hypersurface singularity’, Pure Appl. Math. Q. 12(1) (2016), 165–181.Google Scholar
Yoshinaga, E. and Suzuki, M., ‘Topological types of quasihomogeneous singularities in ℂ2 ’, Topology 18(2) (1979), 113–116.CrossRefGoogle Scholar
Yu, Y., ‘On Jacobian ideals invariant by reducible sl (2; C) action’, Trans. Amer. Math. Soc. 348 (1996), 2759–2791.Google Scholar