No CrossRef data available.
Published online by Cambridge University Press: 01 August 2008
Let ρ be a supernilpotent radical. Let ρ* be the class of all rings A such that either A is a simple ring in ρ or the factor ring A/I is in ρ for every nonzero ideal I of A and every minimal ideal M of A is in ρ. Let 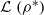 be the lower radical determined by ρ* and let ρφ denote the upper radical determined by the class of all subdirectly irreducible rings with ρ-semisimple hearts. Le Roux and Heyman proved that
be the lower radical determined by ρ* and let ρφ denote the upper radical determined by the class of all subdirectly irreducible rings with ρ-semisimple hearts. Le Roux and Heyman proved that 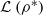 is a supernilpotent radical with
is a supernilpotent radical with 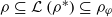 and they asked whether
and they asked whether 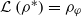 if ρ is replaced by β, ℒ , 𝒩or 𝒥 , where β, ℒ , 𝒩and 𝒥denote the Baer, the Levitzki, the Koethe and the Jacobson radical, respectively. In the present paper we will give a negative answer to this question by showing that if ρ is a supernilpotent radical whose semisimple class contains a nonzero nonsimple * -ring without minimal ideals, then
if ρ is replaced by β, ℒ , 𝒩or 𝒥 , where β, ℒ , 𝒩and 𝒥denote the Baer, the Levitzki, the Koethe and the Jacobson radical, respectively. In the present paper we will give a negative answer to this question by showing that if ρ is a supernilpotent radical whose semisimple class contains a nonzero nonsimple * -ring without minimal ideals, then 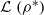 is a nonspecial radical and consequently
is a nonspecial radical and consequently 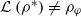 . We recall that a prime ring A is a * -ring if A/I is in β for every
. We recall that a prime ring A is a * -ring if A/I is in β for every 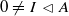 .
.