Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shparlinski, Igor E.
2006.
On the set of distances between two sets over finite fields.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,
IOSEVICH, A.
and
RUDNEV, M.
2009.
FREIMAN THEOREM, FOURIER TRANSFORM AND ADDITIVE STRUCTURE OF MEASURES.
Journal of the Australian Mathematical Society,
Vol. 86,
Issue. 1,
p.
97.
Katz, Nicholas M.
Shparlinski, Igor E.
and
Xiong, Maosheng
2009.
On character sums with distances on the upper half plane over a finite field.
Finite Fields and Their Applications,
Vol. 15,
Issue. 6,
p.
738.
VINH, LE ANH
2011.
ON SUM OF PRODUCTS AND THE ERDŐS DISTANCE PROBLEM OVER FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 84,
Issue. 1,
p.
1.
Shparlinski, Igor E.
2016.
On the additive energy of the distance set in finite fields.
Finite Fields and Their Applications,
Vol. 42,
Issue. ,
p.
187.


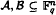 where
where 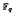 is a finite field of
is a finite field of 