Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-03T20:40:02.294Z Has data issue: false hasContentIssue false
  • English
  • Français

On powerful and p-central restricted Lie algebras

Published online by Cambridge University Press:  17 April 2009

S. Siciliano  and
Th. Weigel
S. Siciliano
Affiliation:
Dipartimento di Matematica “E. De Giorgi”, Universitá di Lecce, Via prov. Lecce-Arnesano, 73100 Lecce, Italy, e-mail: [email protected]
Th. Weigel
Affiliation:
Universitá di Milano-Bicocca, U5–3067, Via R.Cozzi, 53, 20125 Milano, Italy, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we analyse the analogy between m-potent and p-central restricted Lie algebras and p-groups. For restricted Lie algebras the notion of m-potency has stronger implications than for p-groups (Theorem A). Every finite-dimensional restricted Lie algebra  is isomorphic to 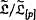for some finite-dimensional p-central restricted Lie algebra 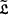(Proposition B). In particular, for restricted Lie algebras there does not hold an analogue of J.Buckley's theorem. For p odd one can characterise powerful restricted Lie algebras in terms of the cup product map in the same way as for finite p-groups (Theorem C). Moreover, the p-centrality of the finite-dimensional restricted Lie algebra  has a strong implication on the structure of the cohomology ring H•(,) (Theorem D).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 75 , Issue 1 , February 2007 , pp. 27 - 44
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Benson, D.J., Representations and cohomology. I, Cambridge Studies in Advanced Mathematics 30 (Cambridge University Press, Cambridge, 1991).Google Scholar
[2]Benson, D.J., Representations and cohomology. II, Cambridge Studies in Advanced Mathematics 31 (Cambridge University Press, Cambridge, 1991).Google Scholar
[3]Benson, D.J. and Carlson, J.F., ‘Projective resolutions and Poincaré duality complexes’, Trans. Amer. Math. Soc. 342 (1994), 447–488.Google Scholar
[4]Berkson, A.J., ‘The u-algebra of a restricted Lie algebra is Fobenius’, Proc. Amer. Math. Soc. 15 (1964), 14–15.Google Scholar
[5]Bianchi, M., Mauri, A. Gillio Berta and Verardi, L., ‘Groups in which elements with the same p-power permute’, Matematiche (Catania) 51 (1996). suppl. (1997) 53–61Google Scholar
[6]Broto, C. and Henn, H-W., ‘Some remarks on central elementary abelian p-subgroups and cohomology of classifying spaces’, Quart. J. Math. Oxford Ser. (2) 44 (1993), 155–163.CrossRefGoogle Scholar
[7]Buckley, J., ‘Finite groups whose minimal subgroups are normal’, Math. Z. 116 (1970), 15–17.Google Scholar
[8]Du, X.K., ‘The centers of a radical ring’, Canad. Math. Bull. 35 (1992), 174–179.CrossRefGoogle Scholar
[9]González-Sánchez, J. and Jaikin-Zapirain, A., ‘On the structure of normal subgroups of potent p-groups‘, J. Algebra 276 (2004), 193–209.CrossRefGoogle Scholar
[10]Hochschild, G., ‘Cohomology of restricted Lie algebras’, Amer. J. Math. 76 (1954), 555–580.CrossRefGoogle Scholar
[11]Jantzen, J.C., ‘Kohomologie von p-Lie-Algebren und nilpotente Elemente’, Abh. Math. Sem. Univ. Hamburg 56 (1986), 191–219.Google Scholar
[12]Jantzen, J.C., ‘Restricted Lie algebra cohomology’, in Algebraic groups Utrecht 1986, Lecture Notes in Math. 1271 (Springer-Verlag, Berlin, 1987), pp. 91–108.CrossRefGoogle Scholar
[13]Kelarev, A.V., ‘Directed graphs and Lie superalgebras of matrices’, J. Algebra 285 (2005), 1–10.CrossRefGoogle Scholar
[14]Kelarev, A.V., Ring constructions and applications, Series in Algebra 9 (World Scientific Publishing Co. Inc., River Edge, NJ, 2002).Google Scholar
[15]Lubotzky, A. and Mann, A., ‘Powerful p-groups. I. Finite groups’, J. Algebra 105 (1987), 484–505.CrossRefGoogle Scholar
[16]Lubotzky, A. and Mann, A., ‘Powerful p-groups. II. p-adic analytic groups’, J. Algebra 105, 506–515.CrossRefGoogle Scholar
[17]Milnor, J.W. and Moore, J.C., ‘On the structure of Hopf algebras’, Ann. of Math. (2) 81 (1965), 211–264.CrossRefGoogle Scholar
[18]Quillen, D., ‘The spectrum of an equivariant cohomology ring. I, II’, Ann. of Math. (2) 94 (1971), 549–572. Ann. of Math. (2) 94 (1971), 573–602.CrossRefGoogle Scholar
[19]Riley, D.M. and Semple, J.F., ‘Completion of restricted Lie algebras’, Israel J. Math. 86 (1994), 277–299.CrossRefGoogle Scholar
[20]Riley, D.M. and Shalev, A., ‘The Lie structure of enveloping algebras’, J. Algebra 162 (1993), 46–61.CrossRefGoogle Scholar
[21]Riley, D.M. and Shalev, A., ‘Restricted Lie algebras and their envelopes’, Canad. J. Math. 47 (1995), 146–164.CrossRefGoogle Scholar
[22]Riley, D.M. and Tasić, V., ‘Lie identities for Hopf algebras’, J. Pure Appl. Algebra 122 (1997), 127–134.CrossRefGoogle Scholar
[23]Siciliano, S., ‘Lie derived lengths of restricted universal enveloping algebras’, Publ. Math. Debrecen 68 (2006), 503–513.Google Scholar
[24]Siciliano, S. and Spinelli, E., ‘Lie nilpotency indices of restricted universal enveloping algebras’, Comm. Algebra 34 (2006), 151–157.Google Scholar
[25]Siciliano, S. and Spinelli, E., ‘Lie metabelian restricted universal enveloping algebras’, Arch. Math. (Basel) 84 (2005), 398–405.CrossRefGoogle Scholar
[26]Strade, H. and Farnsteiner, R., Modular Lie algebras and their representations, Monographs and Textbooks in Pure and Applied Mathematics 116 (Marcel Dekker Inc., New York, 1988).Google Scholar
[27]Symonds, P. and Weigel, Th., ‘Cohomology of p-adic analytic groups’, in New horizons in pro-p groups, (duSautoy, M., Segal, D. and Shalev, A., Editors), Progress in Mathematics 184 (Birkhäuser, Boston, 2000), pp. 349–410.CrossRefGoogle Scholar
[28]Weigel, Th., ‘p-central groups and Poincaré duality’, Trans. Amer. Math. Soc. 352 (2000), 4143–4154.CrossRefGoogle Scholar