Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T02:43:44.422Z Has data issue: false hasContentIssue false
  • English
  • Français

On Positivity of Fourier Transforms

Published online by Cambridge University Press:  17 April 2009

E.O. Tuck
E.O. Tuck
Affiliation:
Applied MathematicsThe University of AdelaideAustralia5005
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

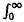This note concerns Fourier transforms on the real positive line. In particular, we seek conditions on a real function u(x) in x > 0, that ensure that its Fourier-cosine transform v(t) = u(x) cos xt dx is positive. We prove first that this is so for all t > 0, if u"(x) > 0 for all x > 0, that is, that everywhere-convex functions have everywhere-positive Fourier-cosine transforms. We then obtain a complex-plane criterion for some types of non-convex u(x). Finally we consider criteria on u(x) that imply positivity of v(t) for t > t0, for some t0 > 0.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 74 , Issue 1 , August 2006 , pp. 133 - 138
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Abramowitz, M. and Stegun, I.A., Handbook of mathematical functions, with formulas, graphs and mathematical tables (Dover Publications, New York, 1964).Google Scholar
[2]Edwards, H.M., Riemann's zeta function (Academic Press, New York, 1974).Google Scholar
[3]Hill, J.M., ‘On some integrals involving functions Φ(x) such that Φ(l/x) = , J. Math. Anal. Appl. 309 (2005), 256–270.CrossRefGoogle Scholar
[4]Tuck, E.O., ‘When does the first derivative exceed the geometric mean of a function and its second derivative?’, Austral. Math. Soc. Gaz. 32 (2005), 267–268.Google Scholar