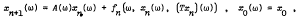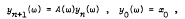Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pachpatte, B. G.
1977.
On discrete inequalities related to Gronwall’s inequality.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 85,
Issue. 1,
p.
26.
Salem, Sh.
1997.
On Some Systems of Two Discrete Inequalities of Gronwall Type.
Journal of Mathematical Analysis and Applications,
Vol. 208,
Issue. 2,
p.
553.
Wang, Wu Sheng
Wang, Ming Jian
and
Lin, Yuan Hua
2013.
On Boundedness of Random Solutions of Perturbed Stochastic Discrete Systems.
Advanced Materials Research,
Vol. 860-863,
Issue. ,
p.
2808.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
423.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
535.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
375.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
345.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
1.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
765.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
233.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
989.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
1.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
885.