Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-23T18:12:41.285Z Has data issue: false hasContentIssue false
  • English
  • Français

On near-rings in which the constants form an ideal

Published online by Cambridge University Press:  17 April 2009

Peter Fuchs
Peter Fuchs
Affiliation:
Institut für Mathematik, Johannes Kepler Universität Linz, A-4040 LinzAustria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let C denote the class of all near-rings which have the property that the subnear-ring of constants forms an ideal. Prominent examples are abstract affine near-rings and a generalisation of these by Feigelstock [1]. In this note we show C forms a variety and construct a proper sub-class 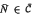such that every N ε C can be embedded into some 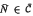. It turns out that near-rings 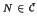have an ideal structure which is similar to the ideal structure of abstract affine near-rings, in contrast to the situation for arbitrary elements of C.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 39 , Issue 2 , April 1989 , pp. 171 - 175
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Feigelstock, S., ‘The near-ring of generalized affine transformations’, Bull. Austral. Math. Soc. 32 (1985), 345–349.CrossRefGoogle Scholar
[2]Pilz, G., Near-rings, 2nd Edition (North Holland, Amsterdam, 1983).Google Scholar