Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T01:44:05.489Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LINEAR COMPLEMENTARY DUAL FOUR CIRCULANT CODES

Part of: Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  29 April 2018

HONGWEI ZHU Open the ORCID record for HONGWEI ZHU [Opens in a new window]  and
MINJIA SHI Open the ORCID record for MINJIA SHI [Opens in a new window]
HONGWEI ZHU
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei, Anhui 230601, China email [email protected]
MINJIA SHI*
Affiliation:
Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, No. 3 Feixi Road, Hefei, Anhui Province 230039, PR China School of Mathematical Sciences of Anhui University, Anhui 230601, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study linear complementary dual four circulant codes of length 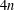$4n$ over 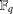$\mathbb{F}_{q}$ when 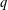$q$ is an odd prime power. When 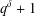$q^{\unicode[STIX]{x1D6FF}}+1$ is divisible by $n$, we obtain an exact count of linear complementary dual four circulant codes of length 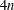$4n$ over 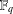$\mathbb{F}_{q}$. For certain values of $n$ and 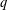$q$ and assuming Artin’s conjecture for primitive roots, we show that the relative distance of these codes satisfies a modified Gilbert–Varshamov bound.

Keywords

four circulant codeslinear complementary dual (LCD) codesArtin’s conjectureChinese remainder theorem

MSC classification

Primary: 94B05: Linear codes, general
Secondary: 94B15: Cyclic codes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 159 - 166
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research is supported by the National Natural Science Foundation of China (61672036), Technology Foundation for Selected Overseas Chinese Scholar, Ministry of Personnel of China (05015133) and Key Projects of Support Program for Outstanding Young Talents in Colleges and Universities (gxyqZD2016008).

References

Alahmadi, A., Güneri, C., Özkaya, B., Shoaib, H. and Solé, P., ‘On self-dual double negacirculant codes’, Discrete Appl. Math. 222 (2017), 205–212.Google Scholar
Alahmadi, A., Ozdemir, F. and Solé, P., ‘On self-dual double circulant codes’, Des. Codes Cryptogr. (to appear), doi:10.1007/s10623-017-0393-x.Google Scholar
Betsumiya, K., Georgiou, S., Gulliver, T. A., Harada, M. and Koukouvinos, C., ‘On self-dual codes over some prime fields’, Discrete Math. 262 (2003), 37–58.Google Scholar
Carlet, C. and Guilley, S., ‘Complementary dual codes for counter-measures to side-channel attacks’, Amer. Inst. Math. Sci. 10(1) (2016), 131–150.Google Scholar
Güneri, C., Özkaya, B. and Solé, P., ‘Quasi-cyclic complementary dual codes’, Finite Fields Appl. 42 (2016), 67–80.Google Scholar
Hooley, C., ‘On Artin’s conjecture’, J. reine angew. Math. 225 (1967), 209–220.Google Scholar
Huffman, W. C. and Pless, V., Fundamentals of Error Correcting Codes (Cambridge University Press, New York, NY, 2003).Google Scholar
Kaya, A., Yildiz, B. and Pasa, A., ‘New extremal binary self-dual codes from a modified four circulant construction’, Discrete Math. 339 (2016), 1086–1094.CrossRefGoogle Scholar
Lidl, R. and Niederreiter, H., Finite Fields (Addison-Wesley, Reading, MA, 1983).Google Scholar
Ling, S. and Solé, P., ‘On the algebraic structure of quasi-cyclic codes I: finite fields’, IEEE Trans. Inform. Theory 47(7) (2001), 2751–2760.Google Scholar
Massey, J. L., ‘Linear codes with complementary duals’, Discrete Math. 106–107 (1992), 337–342.Google Scholar
Moree, P., ‘Artin’s primitive root conjecture - a survey’, Integers 10(6) (2012), 1305–1416.Google Scholar
Shi, M. J., Qian, L. Q. and Solé, P., ‘On the self-dual negacirculant codes of index two and four’, Des. Codes Cryptogr. (to appear), doi:10.1007/s10623-017-0455-0.Google Scholar
Shi, M. J., Zhu, H. W. and Solé, P., ‘On the self-dual four-circulant codes’, Internat. J. Found. Comput. Sci. (to appear), https://arxiv.org/pdf/1709.07548.pdf (2017).Google Scholar