Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T21:00:02.426Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GRAPHS OF PRIME VALENCY ADMITTING A SOLVABLE ARC-TRANSITIVE GROUP

Part of: Algebraic combinatorics Permutation groups

Published online by Cambridge University Press:  13 May 2015

BOŠTJAN KUZMAN
BOŠTJAN KUZMAN*
Affiliation:
University of Ljubljana, Faculty of Education, Department of Math and Computer Science, Kardeljeva ploščad 16, 1000 Ljubljana, Slovenia Institute of Mathematics, Physics and Mechanics, Jadranska 19, 1000 Ljubljana, Slovenia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 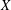$X$ be a simple, connected, 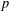$p$-valent, 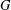$G$-arc-transitive graph, where the subgroup 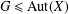$G\leq \text{Aut}(X)$ is solvable and 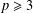$p\geq 3$ is a prime. We prove that 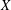$X$ is a regular cover over one of the three possible types of graphs with semi-edges. This enables short proofs of the facts that 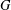$G$ is at most 3-arc-transitive on 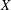$X$ and that its edge kernel is trivial. For pentavalent graphs, two further applications are given: all 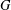$G$-basic pentavalent graphs admitting a solvable arc-transitive group are constructed and an example of a non-Cayley graph of this kind is presented.

Keywords

arc-transitive graphssolvable groupedge kernelpentavalent graphs

MSC classification

Primary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Secondary: 05E18: Group actions on combinatorial structures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 214 - 227
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bosma, W., Cannon, C. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Feng, Y.-Q., Li, C. H. and Zhou, J.-X., ‘Symmetric cubic graphs with solvable automorphism groups’, European J. Combin. 45 (2015), 1–11.CrossRefGoogle Scholar
Lorimer, P., ‘Vertex-transitive graphs, symmetric graphs of prime valency’, J. Graph Theory 8 (1984), 55–68.CrossRefGoogle Scholar
Malnič, A., ‘Action graphs and coverings’, Discrete Math. 244 (2002), 299–322.CrossRefGoogle Scholar
Malnič, A., Marušič, D. and Potočnik, P., ‘Elementary abelian covers of graphs’, J. Algebraic Combin. 20 (2004), 71–97.CrossRefGoogle Scholar
Malnič, A., Marušič, D. and Potočnik, P., ‘On cubic graphs admitting an edge-transitive solvable group’, J. Algebraic Combin. 20 (2004), 99–113.CrossRefGoogle Scholar
Morgan, G. L., ‘On symmetric and locally finite actions of groups on the quintic tree’, Discrete Math. 313(21) (2013), 2486–2492.CrossRefGoogle Scholar
Potočnik, P., Spiga, P. and Verret, G., ‘On the order of arc-stabilisers in arc-transitive graphs with prescribed local group’, Trans. Amer. Math. Soc. 366 (2014), 3729–3745.CrossRefGoogle Scholar
Požar, R., ‘Some computational aspects of solvable regular covers of graphs’, J. Symbolic Comput. 70(September–October) (2015), 1–13.CrossRefGoogle Scholar
Verret, G., ‘On the order of arc-stabilizers in arc-transitive graphs’, Bull. Aust. Math. Soc. 80(3) (2009), 498–505.CrossRefGoogle Scholar
Verret, G., ‘On the order of arc-stabilisers in arc-transitive graphs, II’, Bull. Aust. Math. Soc. 87(3) (2013), 441–447.CrossRefGoogle Scholar
Weiss, R., ‘An application of p-factorization methods to symmetric graphs’, Math. Proc. Cambridge Philos. Soc. 85 (1979), 43–48.CrossRefGoogle Scholar
Weiss, R., ‘s-transitive graphs’, in: Algebraic Methods in Graph Theory, Vols. I, II (Szeged, 1978), Colloquia Mathematica Societatis János Bolyai, 25 (North-Holland, Amsterdam, 1981), 827–847.Google Scholar
Weisstein, E. W., ‘Clebsch Graph’, from MathWorld–A Wolfram Web Resource.http://mathworld.wolfram.com/ClebschGraph.html.Google Scholar