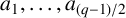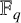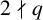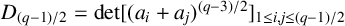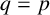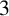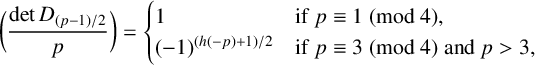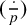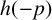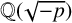1 Introduction
1.1 Related work and motivations
Let p be an odd prime and let
$(\frac {\cdot }{p})$
be the Legendre symbol. Chapman [Reference Chapman1, Reference Chapman2] investigated determinants involving Legendre matrices
$$ \begin{align*}C_1=\bigg[\bigg(\frac{i+j-1}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}\end{align*} $$
and
$$ \begin{align*}C_2=\bigg[\bigg(\frac{i+j-1}{p}\bigg)\bigg]_{1\le i,j\le (p+1)/2}.\end{align*} $$
Surprisingly, these determinants are closely related to quadratic fields. In fact, letting
$\varepsilon _p>1$
and
$h(p)$
be the fundamental unit and the class number of
$\mathbb {Q}(\sqrt {p})$
, and writing
$\varepsilon _p=a_p+b_p\sqrt {p}$
with
$a_b,b_p\in \mathbb {Q}$
, Chapman [Reference Chapman1] proved that
$$ \begin{align*}\det C_1= \begin{cases} (-1)^{(p-1)/4}2^{(p-1)/2}b_p & \mbox{if}\ p\equiv1\pmod4,\\ 0 & \mbox{otherwise,} \end{cases}\end{align*} $$
and
$$ \begin{align*}\det C_2= \begin{cases} (-1)^{(p+3)/4}2^{(p-1)/2}a_p & \mbox{if}\ p\equiv1\pmod4,\\ -2^{(p-1)/2} & \mbox{otherwise.} \end{cases}\end{align*} $$
Later, Chapman [Reference Chapman2] posed the following conjecture.
Conjecture 1.1 (Chapman).
Let p be an odd prime and write
$\varepsilon _p^{(2-(2/p))h(p)}= a_p^{\prime } +b_p^{\prime }\sqrt {p}$
with
$a_p^{\prime },b_p^{\prime }\in \mathbb {Q}$
. Then
$$ \begin{align*}\det \bigg[\bigg(\frac{j-i}{p}\bigg)\bigg]_{1\le i,j\le (p+1)/2} =\begin{cases} -a_p^{\prime} & \mbox{if}\ p\equiv1\pmod 4,\\ 1 & \mbox{otherwise.} \end{cases}\end{align*} $$
Due to the difficulty of the conjecture, Chapman called this determinant ‘the evil determinant’. In 2012 and 2013, Vsemirnov [Reference Vsemirnov9, Reference Vsemirnov10] confirmed the conjecture (the case
$p\equiv 3\pmod 4$
in [Reference Vsemirnov9] and the case
$p\equiv 1\pmod 4$
in [Reference Vsemirnov10]).
In 2019, Sun [Reference Sun8] studied some variants of Chapman’s determinants. For example, let
$$ \begin{align*} S(d,p)=\det\bigg[\bigg(\frac{i^2+dj^2}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}.\end{align*} $$
Sun [Reference Sun8, Theorem 1.2] showed that
$S(d,p)=0$
whenever
$(d/p)=-1$
and that
$(-S(d,p)/p)=1$
whenever
$(d/p)=1$
. (See [Reference Krachun, Petrov, Sun and Vsemirnov3, Reference Li and Wei5, Reference Wu11, Reference Wu, She and Wang13] for recent progress on this topic.) Also, Sun [Reference Sun8, Theorem 1.4] proved that
$$ \begin{align} \det\bigg[\frac{((i+j)/p)}{i+j}\bigg]_{1\le i,j\le (p-1)/2} \equiv\begin{cases} (2/p)\pmod p & \mbox{if}\ p\equiv1\pmod4,\\ ((p-1)/2)!\pmod p & \mbox{otherwise,} \end{cases} \end{align} $$
and that
$$ \begin{align*} \det\bigg[\frac{1}{i^2+j^2}\bigg]_{1\le i,j\le (p-1)/2}\equiv (-1)^{{(p+1)}/{4}}\pmod p \end{align*} $$
whenever
$p\equiv 3\pmod 4$
. In 2022, the third author and Wang [Reference Wu and Wang14, Theorem 1.7] considered the determinant
$\det [1/(\alpha _i+\alpha _j)]_{1\le i,j\le (p-1)/k}$
, where
$0<\alpha _1,\ldots ,\alpha _{(p-1)/k}<p$
are all the kth power residues modulo p and showed that for any positive even integer k such that
$k\mid p-1$
, if
$-1$
is not a kth power modulo p, then
$$ \begin{align*} \det\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m} \equiv \frac{(-1)^{(m+1)/2}}{(2k)^m}\pmod p, \end{align*} $$
where
$m=(p-1)/k$
.
Now let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. It is known that
$\mathbb {F}_q^{\times }=\mathbb {F}_q\setminus \{0\}$
is a cyclic group of order
$q-1$
and that the subgroups
$$ \begin{align*}U_k=\{x\in\mathbb{F}_q: x^k=1\}=\{a_1,\ldots,a_k\}\quad (k\ge 1, k\mid q-1)\end{align*} $$
are exactly all subgroups of
$\mathbb {F}_q^{\times }$
. Let
$\phi $
be the unique quadratic character of
$\mathbb {F}_q$
, that is,
$$ \begin{align*}\phi(x)=\begin{cases} 1 & \mbox{if}\ x\ \text{is a nonzero square},\\ 0 & \mbox{if}\ x=0,\\ -1 & \mbox{otherwise.} \end{cases}\end{align*} $$
As
$\mathrm {char}(\mathbb {F}_q)>2$
, the subset
$\{\pm 1\}\subseteq \mathbb {Z}$
can be viewed as a subset of
$\mathbb {F}_q$
. From now on, we always assume
$\pm 1\in \mathbb {F}_q$
. Inspired by Sun’s determinant (1.1), it is natural to consider the matrix
$$ \begin{align*} \bigg[\frac{\phi(a_i+a_j)}{a_i+a_j}\bigg]_{1\le i,j\le k}. \end{align*} $$
However, if
$k\mid q-1$
is even, then the denominator
$a_i+a_j=0$
for some
$i,j$
since
${-1\in U_k}$
in this case. To overcome this obstacle, note that for any
$x\in \mathbb {F}_q$
, we have
$\phi (x)=x^{(q-1)/2}$
. Hence, we first focus on the matrix
$$ \begin{align*} D_k:=[(a_i+a_j)^{(q-3)/2}]_{1\le i,j\le k}. \end{align*} $$
The main results involving
$D_k$
will be given in Section 1.2.
We now consider another type of determinant. Sun [Reference Sun8, Remark 1.3] posed the following conjecture.
Conjecture 1.2 (Sun).
Let
$p\equiv 2\pmod 3$
be an odd prime. Then
$$ \begin{align} 2\det\bigg[\frac{1}{i^2-ij+j^2}\bigg]_{1\le i,j\le p-1} \end{align} $$
is a quadratic residue modulo p.
The third author, She and Ni [Reference Wu, She and Ni12] obtained the following generalised result.
Theorem 1.3 (Wu, She and Ni).
Let
$q\equiv 2\pmod 3$
be an odd prime power. Let
$\beta _1,\ldots ,\beta _{q-1}$
be all the nonzero elements of
$\mathbb {F}_q$
. Then
$$ \begin{align*}\det\bigg[\frac{1}{\beta_i^2-\beta_i\beta_j+\beta_j^2}\bigg]_{1\le i,j\le q-1} =(-1)^{(q+1)/2}2^{(q-2)/3}\in\mathbb{F}_p, \end{align*} $$
where
$p=\mathrm {char}(\mathbb {F}_q)$
.
Recently, Luo and Sun [Reference Luo and Sun6] investigated the determinant
$$ \begin{align} \det S_p(c,d)=\det[(i^2+cij+dj^2)^{p-2}]_{1\le i,j\le p-1}. \end{align} $$
For
$(c,d)=(1,1)$
or
$(2,2)$
, they determined the explicit values of
$({\det S_p(c,d)}/{p})$
.
Motivated by Sun’s determinants (1.1)–(1.3) and the above discussions, we also consider the matrix
$$ \begin{align*}T_k:=[(a_i^2+a_ia_j+a_j^2)^{(q-3)/2}]_{1\le i,j\le k}.\end{align*} $$
We will state our results concerning
$T_k$
in Section 1.3.
1.2 The main results involving det
$\,D_k$
Theorem 1.4. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. Then for any integer
$k\mid q-1$
with
$1<k\le q-1$
,
$$ \begin{align*}\det D_k=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot k^k\in\mathbb{F}_p,\end{align*} $$
where
$$ \begin{align*}w_k=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\in\mathbb{F}_p.\end{align*} $$
Suppose now that
$k=(q-1)/2$
, that is,
$U_{(q-1)/2}$
is the set of all the nonzero squares over
$\mathbb {F}_q$
. Then we can obtain the following simplified result which will be proved in Section 2.
Corollary 1.5. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. Then
$$ \begin{align*}\det D_{(q-1)/2}= \begin{cases} (-1)^{({q+3})/{4}}u^2 & \mbox{if}\ q\equiv 1\pmod4,\\ (-1)^{({q+5})/{4}}\binom{(q-3)/2}{(q-3)/4}v^2 & \mbox{if}\ q\equiv 3\pmod4\ \text{and}\ q>3, \end{cases}\end{align*} $$
where
$u,v\in \mathbb {F}_p$
are defined by
$$ \begin{align*}u=\prod_{s=0}^{(q-5)/4}\binom{(q-3)/2}{s}\quad \text{and}\quad v=\prod_{s=0}^{(q-7)/4}\binom{(q-3)/2}{s}.\end{align*} $$
In particular, if
$q=p>3$
is an odd prime, then
$D_{(p-1)/2}$
is nonsingular and
$$ \begin{align*}\bigg(\frac{\det D_{(p-1)/2}}{p}\bigg)= \begin{cases} 1 & \mbox{if}\ p\equiv1\pmod4,\\ (-1)^{(h(-p)+1)/2} & \mbox{if}\ p\equiv 3\pmod4\ \text{and}\ p>3, \end{cases}\end{align*} $$
where
$h(-p)$
is the class number of
$\mathbb {Q}(\sqrt {-p})$
.
From Theorem 1.4, we see that
$\det D_k\in \mathbb {F}_p$
. The next result gives the explicit value of
$({\det D_k}/{p})$
when k is odd.
Theorem 1.6. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. Let
${1<k\le q-1}$
be an odd integer with
$k\mid q-1$
. Suppose that
$D_k$
is nonsingular. Then
$$ \begin{align*} \bigg(\frac{\det D_k}{p}\bigg)=\bigg(\frac{s_k}{p}\bigg), \end{align*} $$
where
$$ \begin{align*} s_k:=k\sum_{r=1}^{({q-1)}/{2k}}\binom{(q-3)/2}{((2r-1)k-1)/2}\in\mathbb{F}_p.\end{align*} $$
1.3 The main results involving
$\mathrm{det}\ T_k$
To state the next results, we need to introduce some basic properties of trinomial coefficients. Let n be a positive integer. For any integer r, the trinomial coefficient
$\binom {n}{r}_2$
is defined by
$$ \begin{align*}\bigg(x+\frac{1}{x}+1\bigg)^{n}= \sum_{r=-\infty}^{+\infty}\binom{n}{r}_2x^r.\end{align*} $$
This implies that
$\binom {n}{r}_2=0$
whenever
$|r|>n$
and that
$\binom {n}{r}_2=\binom {n}{-r}_2$
for any integer r. In particular,
$\binom {n}{0}_2$
is usually called the central trinomial coefficient because
$\binom {n}{0}_2$
is exactly the coefficient of
$x^n$
in the polynomial
$(x^2+x+1)^n$
. For simplicity,
$\binom {n}{0}_2$
is also denoted by
$t_n$
.
Theorem 1.7. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. Then for any integer
$k\mid q-1$
with
$1<k\le q-1$
,
$$ \begin{align*}\det T_k=l_k\cdot k^k\in\mathbb{F}_p,\end{align*} $$
where
$$ \begin{align*}l_k=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{(q-3)/2-s-kr}_2\in\mathbb{F}_p.\end{align*} $$
As a direct consequence of Theorem 1.7, we have the following result.
Corollary 1.8. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
. For any integer
$k\mid q-1$
with
$1<k\le q-1$
, the matrix
$T_k$
is singular over
$\mathbb {F}_q$
if and only if
$$ \begin{align*} \sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{(q-3)/2-s-kr}_2\equiv0\pmod p\end{align*} $$
for some s with
$0\le s\le k-1$
. In particular,
$T_{q-1}$
is a singular matrix over
$\mathbb {F}_q$
.
In the case
$k=(q-1)/2$
, similar to Corollary 1.5, by Theorem 1.7, we deduce the following simplified result.
Corollary 1.9. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p>2$
.
-
(i) If
$q\equiv 1\pmod 4$
, then
$$ \begin{align*}\det T_{(q-1)/2}= \prod_{s=0}^{(q-5)/4} \bigg(\binom{(q-3)/2}{(q-3)/2-s}_2+\binom{(q-3)/2}{1+s}_2\bigg)^2.\end{align*} $$
-
(ii) If
$q\equiv 3\pmod 4$
and
$q>3$
, then
$$ \begin{align*}\det T_{(q-1)/2}= \binom{(q-3)/2}{0}_2\prod_{s=0}^{(q-7)/4} \Bigg(\binom{(q-3)/2}{(q-3)/2-s}_2+\binom{(q-3)/2}{1+s}_2\Bigg)^2.\end{align*} $$
In particular, if
$T_{(q-1)/2}$
is nonsingular, then
$$ \begin{align*} \bigg(\frac{\det T_{(q-1)/2}}{p}\bigg)=\begin{cases} (-1)^{(q-1)/4} & \mbox{if}\ q\equiv1\pmod4,\\ \bigg(\dfrac{t_{(q-3)/2}}{p}\bigg)(-1)^{(q+5)/4} & \mbox{if}\ q\equiv3\pmod4\ \text{and}\ q>3. \end{cases} \end{align*} $$
2 Proofs of Theorem 1.4 and Corollary 1.5
We begin with the following result (see [Reference Krattenthaler4, Lemma 10]).
Lemma 2.1. Let R be a commutative ring. Let
$P(t)=p_0+p_1t+\cdots +p_{n-1}t^{n-1}\in R[t]$
. Then
$$ \begin{align*}\det[P(X_iY_j)]_{1\le i,j\le n}=\prod_{i=0}^{n-1}p_i \cdot \prod_{1\le i<j\le n}(X_j-X_i)(Y_j-Y_i).\end{align*} $$
We also need the following result.
Lemma 2.2. Let
$\mathbb {F}_q$
be the finite field of q elements with
$\mathrm {char}(\mathbb {F}_q)=p$
. For any positive integer
$k\mid q-1$
, if we set
$U_k=\{a_1,\ldots ,a_k\}$
, then
$$ \begin{align*}\prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=k^k\in\mathbb{F}_p.\end{align*} $$
Proof. It is clear that
$$ \begin{align} \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg) =\prod_{1\le i<j\le k}\frac{(a_j-a_i)(a_i-a_j)}{a_ia_j} =\prod_{1\le i\neq j\le k}(a_j-a_i) \prod_{1\le i<j\le k}\frac{1}{a_ia_j}. \end{align} $$
Let
$S_1=\prod _{1\le i\neq j\le k}(a_j-a_i)$
and let
$S_2=\prod _{1\le i<j\le k}{1}/{(a_ia_j)}$
. We first consider
$S_1$
. Let
$$ \begin{align*}G_k(t)=\prod_{i=1}^k(t-a_i)\in\mathbb{F}_q[t]\end{align*} $$
and let
$G^{\prime }_k(t)$
be the formal derivative of
$G_k(t)$
. Then by the definition of
$U_k$
, we see that
$G_k(t)=t^k-1$
. Thus,
$G_k^{\prime }(t)=kt^{k-1}$
and
$\prod _{1\le j\le k}a_j=(-1)^{k+1}$
. Now we can verify that
$$ \begin{align} S_1 =\prod_{1\le i\neq j\le k}(a_j-a_i)=\prod_{1\le j\le k}G_k^{\prime}(a_j) =\prod_{1\le j\le k}ka_j^{k-1} =k^k(-1)^{k+1}. \end{align} $$
We turn to
$S_2$
. It is clear that
$$ \begin{align} S_2=\prod_{1\le i<j\le k}\frac{1}{a_ia_j}=\prod_{1\le j\le k}\frac{1}{a_j^{k-1}}=(-1)^{k+1}. \end{align} $$
Combining (2.1) with (2.2) and (2.3),
$$ \begin{align*} \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=S_1S_2=k^k\in\mathbb{F}_p. \end{align*} $$
This completes the proof.
Proof of Theorem 1.4.
As
$\mathrm {char}(\mathbb {F}_q)=p>2$
, the subset
$\{1,-1\}\subseteq \mathbb {Z}$
can be naturally viewed as a subset of
$\mathbb {F}_q$
. One can verify that
$$ \begin{align} \det D_k =\det[(a_i+a_j)^{{(q-3)}/{2}}]_{1\le i,j\le k} &=\prod_{i=1}^ka_i^{{(q-3)}/{2}}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{{(q-3)}/{2}}\bigg]_{1\le i,j\le k}\nonumber\\ &=(-1)^{(k+1)(q-3)/2}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{{(q-3)}/{2}}\bigg]_{1\le i,j\le k}. \end{align} $$
The last equality follows from
$\prod _{1\le j\le k}a_j=(-1)^{k+1}$
. Let
$$ \begin{align*}f_k(t) =\sum_{s=0}^{k-1} \Bigg(\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\Bigg)t^s\in\mathbb{F}_p[t]\end{align*} $$
with
$\deg (f_k)\le k-1$
. Noting that
$(a_j/a_i)^{k+s}=(a_j/a_i)^s$
for any integer s, by (2.4),
$$ \begin{align*} \det D_k =(-1)^{(k+1)(q-3)/2} \cdot \det\bigg[f_k\bigg(\frac{a_j}{a_i}\bigg)\bigg]_{1\le i,j\le k}. \end{align*} $$
Let
$$ \begin{align*}w_k:=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\in\mathbb{F}_p.\end{align*} $$
$$ \begin{align*}\det D_k=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot k^k\in\mathbb{F}_p.\end{align*} $$
This completes the proof.
Proof of Corollary 1.5.
By Theorem 1.4, if
$k=(q-1)/2$
, then
$$ \begin{align} \det D_{(q-1)/2} &=(-1)^{(q-3)/2}\cdot\prod_{s=0}^{(q-3)/2}\binom{(q-3)/2}{s}\cdot (-1)^{(q-1)/2}\bigg(\frac{1}{2}\bigg)^{(q-1)/2}\nonumber\\ &=-1\cdot\prod_{s=0}^{(q-3)/2}\binom{(q-3)/2}{s}\cdot\phi(2). \end{align} $$
The last equality follows from
$$ \begin{align*}(\tfrac{1}{2})^{(q-1)/2}=\phi(\tfrac{1}{2})=\phi(2).\end{align*} $$
We now divide the remaining part of the proof into two cases.
Case 1:
$q\equiv 1\pmod 4$
.
In this case, we have
$\sqrt {-1}\in \mathbb {F}_q$
, where
$\sqrt {-1}$
is an element in the algebraic closure of
$\mathbb {F}_q$
such that
$(\sqrt {-1})^2=-1$
. Since
$2=-\sqrt {-1}(1+\sqrt {-1})^2,$
we have
$\phi (2)=\phi (-\sqrt {-1})$
and hence
$$ \begin{align} \phi(2)=\phi(-\sqrt{-1})=(-\sqrt{-1})^{(q-1)/2}=(-1)^{(q-1)/4}. \end{align} $$
Combining (2.5) with (2.6) and noting that
$$ \begin{align*}\binom{(q-3)/2}{s}=\binom{(q-3)/2}{(q-3)/2-s},\end{align*} $$
we obtain
$$ \begin{align} \det D_{(q-1)/2}=(-1)^{(q+3)/4}\prod_{s=0}^{(q-5)/4}\binom{(q-3)/2}{s}^2. \end{align} $$
This proves the case
$q\equiv 1\pmod 4$
.
Case 2:
$q\equiv 3\pmod 4$
and
$q>3$
.
In this case, since
$q\equiv 3\pmod 4$
,
$(1+\sqrt {-1})^q=1+(\sqrt {-1})^q=1-\sqrt {-1}$
. This, together with
$2=-\sqrt {-1}\big (1+\sqrt {-1}\big )^2$
, implies that
$$ \begin{align} \phi(2) &=2^{(q-1)/2}=(-\sqrt{-1})^{(q-3)/2}(-\sqrt{-1})\big(1+\sqrt{-1}\big)^{q-1}\nonumber\\ &=(-1)^{(q-3)/4}(-\sqrt{-1})\frac{1-\sqrt{-1}}{1+\sqrt{-1}}\nonumber\\ &=(-1)^{(q+1)/4}. \end{align} $$
$$ \begin{align} \det D_{(q-1)/2}=(-1)^{(q+5)/4}\binom{(q-3)/2}{(q-3)/4}\prod_{s=0}^{(q-7)/4}\binom{(q-3)/2}{s}^2. \end{align} $$
This proves the case
$q\equiv 3\pmod 4$
and
$q>3$
.
Now we assume that
$q=p$
is an odd prime. Suppose first
$p\equiv 1\pmod 4$
. Then by (2.7), we see that
$\det D_{(q-1)/2}$
is a nonzero square in
$\mathbb {F}_p$
, that is,
$({\det D_{(p-1)/2}}/{p})=1$
. In the case
$p\equiv 3\pmod 4$
and
$p>3$
, by (2.9) and
$({-2}/{p})=({-\tfrac 12}/{p})=(-1)^{(p+5)/4}$
,
$$ \begin{align*} \bigg(\frac{\det D_{(q-1)/2}}{p}\bigg)&=(-1)^{(p+5)/4}\Bigg(\frac{\tfrac{p-3}{2}!}{p}\Bigg) =(-1)^{(p+5)/4}\Bigg(\frac{\tfrac{p-1}{2}!}{p}\Bigg) \Bigg(\frac{\tfrac{-1}{2}}{p}\Bigg) =\Bigg(\frac{\tfrac{p-1}{2}!}{p}\Bigg) =(-1)^{(h(-p)+1)/2}. \end{align*} $$
The last equality follows from Mordell’s result [Reference Mordell7] which states that
$$ \begin{align*}\frac{p-1}{2}!\equiv (-1)^{{(h(-p)+1)}/{2}}\pmod p\end{align*} $$
whenever
$p\equiv 3\pmod 4$
and
$p>3$
. This completes the proof.
3 Proof of Theorem 1.6
To prove Theorem 1.6, we first need the following well-known result.
Lemma 3.1. Let
$\mathbb {F}_q$
be the finite field of q elements and let r be a positive integer. Then
$$ \begin{align*} \sum_{x\in\mathbb{F}_q}x^r=\begin{cases} 0 & \mbox{if}\ q-1\nmid r,\\ -1 & \mbox{if}\ q-1\mid r. \end{cases} \end{align*} $$
We will see later in the proof that
$\det D_k$
has close relations with the determinant of a circulant matrix. Hence, we now introduce the definition of circulant matrices. Let R be a commutative ring. Let
$b_0,b_1,\ldots ,b_{s-1}\in R$
. We define the circulant matrix
$C(b_0,\ldots ,b_{s-1})$
to be an
$s\times s$
matrix whose (
$i,j$
)-entry is
$b_{j-i}$
where the indices are cyclic module s, that is,
$b_i=b_j$
whenever
$i\equiv j\pmod s$
. The third author [Reference Wu11, Lemma 3.4] obtained the following result.
Lemma 3.2. Let R be a commutative ring. Let s be a positive integer. Let
$b_0,b_1,\ldots ,b_{s-1}\in R$
such that
$b_i=b_{s-i}$
for
$1\leqslant i\leqslant s-1$
.
If s is even, then there exists an element
$u\in R$
such that
$$ \begin{align*} \det C(b_0,\ldots,b_{s-1})=\bigg(\sum_{i=0}^{s-1}b_i\bigg)\bigg(\sum_{i=0}^{s-1}(-1)^ib_i\bigg)\cdot u^2. \end{align*} $$
If s is odd, then there exists an element
$v\in R$
such that
$$ \begin{align*} \det C(b_0,\ldots,b_{s-1})=\bigg(\sum_{i=0}^{s-1}b_i\bigg)\cdot v^2. \end{align*} $$
Proof of Theorem 1.6.
As k is odd, we have
$2\mid (q-1)/k$
. For simplicity, we let
$q-1=nk=2mk$
. Since
$k\mid (q-1)/2$
in this case,
$\phi (a_i)=a_i^{(q-1)/2}=1$
for each
$a_i\in U_k$
. Let g be a generator of the cyclic group
$\mathbb {F}_q^{\times }$
. By the above, one can verify that
$$ \begin{align*} \det D_k =\prod_{i=1}^ka_i^{(q-3)/2}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k} =\det[(1+g^{nj-ni})^{(q-3)/2}]_{0\le i,j\le k-1}. \end{align*} $$
The last equality follows from
$$ \begin{align*} \prod_{i=1}^ka_i=(-1)^{k+1}=1. \end{align*} $$
By the above and using the properties of determinants, one can verify that
$$ \begin{align} \det D_k=\det[(1+g^{nj-ni})^{(q-3)/2}g^{mj-mi}(-1)^{j-i}]_{0\le i,j\le k-1}. \end{align} $$
For
$0\le i\le k-1$
,
$$ \begin{align*}b_i=(1+g^{ni})^{(q-3)/2}g^{mi}(-1)^i.\end{align*} $$
We claim that
$b_i=b_{k-i}$
for
$1\le i\le k-1$
. In fact, for
$1\le i\le k-1$
, noting that
$$ \begin{align*}g^{km}=\phi(g)=-1,\quad g^{nk}=1,\ 2\nmid k \quad \text{and}\quad \bigg(\frac{1}{g^{ni}}\bigg)^{(q-3)/2}=g^{ni},\end{align*} $$
one can verify that
$$ \begin{align*} b_{k-i}&=(1+g^{nk-ni})^{(q-3)/2}g^{mk-mi}(-1)^{k-i}\\ &=\bigg(\frac{1+g^{ni}}{g^{ni}}\bigg)^{(q-3)/2}g^{-mi}(-1)^i\\ &=(1+g^{ni})^{(q-3)/2}g^{(n-m)i}(-1)^i\\ &=b_i. \end{align*} $$
Hence, by (3.1),
$\det D_k=\det C(b_0,b_1,\ldots ,b_{k-1})$
. Now by Lemma 3.2 and (3.1),
$$ \begin{align} \det D_k=\bigg(\sum_{i=0}^{k-1}b_i\bigg)v^2 \end{align} $$
for some
$v\in \mathbb {F}_q$
. Now we consider the sum
$\sum _{i=0}^{k-1}b_i$
. It is easy to verify that
$$ \begin{align} \sum_{i=0}^{k-1}b_i &=\sum_{i=0}^{k-1}(1+g^{ni})^{(q-3)/2}g^{mi}(-1)^i =\sum_{i=0}^{k-1}(1+g^{ni})^{(q-3)/2}g^{mi}g^{mki}\nonumber\\ &=\frac{1}{n}\sum_{x\in\mathbb{F}_q}(1+x^n)^{(q-3)/2}x^{m+mk} =\frac{1}{n}\sum_{r=0}^{mk-1}\binom{(q-3)/2}{r}\sum_{x\in\mathbb{F}_q}x^{m+mk+2mr}. \end{align} $$
Now by Lemma 3.1, since
$2\nmid k$
,
$$ \begin{align*}\sum_{x\in\mathbb{F}_q}x^{m+mk+2mr}=\begin{cases} 0 & \mbox{if}\ k\nmid 1+2r,\\ -1 & \mbox{if}\ k\mid 1+2r. \end{cases} \end{align*} $$
Applying this and Lemma 3.1 to (3.3) and noting that
$-1/n=k$
in
$\mathbb {F}_p$
,
$$ \begin{align} s_k:=\sum_{i=0}^{k-1}b_i=k\sum_{r=1}^m\binom{(q-3)/2}{((2r-1)k-1)/2}. \end{align} $$
Suppose that
$D_k$
is nonsingular. Then by Theorem 1.4, we have
$\det D_k\in \mathbb {F}_p^{\times }$
. Hence, by (3.2) and (3.4),
$$ \begin{align*}\bigg(\frac{\det D_k}{p}\bigg)=\bigg(\frac{s_k}{p}\bigg).\end{align*} $$
This completes the proof.
4 Proof of Theorem 1.7
It is clear that
$$ \begin{align} \det T_k &=\prod_{i=1}^{k}(a_i^2)^{(q-3)/2} \cdot \det\bigg[\bigg(1+\frac{a_j}{a_i}+\bigg(\frac{a_j}{a_i}\bigg)^2\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k}\nonumber\\ &=\det\bigg[\bigg(1+\frac{a_j}{a_i}+\bigg(\frac{a_j}{a_i}\bigg)^2\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k}. \end{align} $$
The last equality follows from
$$ \begin{align*}\prod_{i=1}^ka_i=(-1)^{k+1}.\end{align*} $$
Let
$$ \begin{align*}g_k(t)= \sum_{s=0}^{k-1} \Bigg(\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{s+rk-(q-3)/2}_2\Bigg)t^s\in\mathbb{F}_p[t]\end{align*} $$
with
$\deg (g_k)\le k-1$
. Then by (4.1), Lemma 2.1 and the definition of trinomial coefficients,
$$ \begin{align*} \det T_k &=\det\bigg[g_k\bigg(\frac{a_j}{a_i}\bigg)\bigg]_{1\le i,j\le k}\\ &=\prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)\cdot \prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{s+rk-(q-3)/2}_2\\ &=l_kk^k\in\mathbb{F}_p. \end{align*} $$
The last equality follows from Lemma 2.2. This completes the proof.
$\Box $
Acknowledgement
We would like to thank the referee for helpful comments.
