Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T03:05:33.710Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on simultaneous polynomial approximation of exponential functions

Published online by Cambridge University Press:  17 April 2009

J.H. Loxton  and
A.J. van der Poorten
J.H. Loxton
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
A.J. van der Poorten
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let α1, …, αm be distinct complex numbers and τ(1), …, τ(m) be non-negative integers. We obtain conditions under which the functions

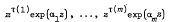
form a perfect system, that is, for every set ρ(1), …, ρ(m) of non-negative integers, there are polynomials a1 (z), …, am (z) with respective degrees exactly ρ(1)−1, …, ρ(m)−1, such that the function

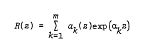
has a zero of order at least ρ(1) + … + ρ(m)−1 at the origin. Moreover, subject to the evaluation of certain determinants, we give explicit formulae for the approximating polynomials a1 (z), …, am (z).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 11 , Issue 3 , December 1974 , pp. 333 - 338
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Baker, A., “On some diophantine inequalities involving the exponential function”, Canad. J. Math. 17 (1965), 616–626.CrossRefGoogle Scholar
[2]Mahler, Kurt, “Zur Approximation der Exponentialfunktion und des Logarithmus. Teil 1”, J. reine angew. Math. 166 (1932), 118–136.Google Scholar
[3]Mahler, Kurt, “Zur Approximation der Exponentialfunktion und des Logarithmus. Teil II”, J. reine angew. Math. 166 (1932), 137–150.CrossRefGoogle Scholar
[4]Mahler, K., “Perfect systems”, Compositio Math. 19 (1968), 95–166.Google Scholar
[5]van der Poorten, A.J., “Perfect approximation of functions”, Bull. Austral. Math. Soc. 5 (1971), 117–126.Google Scholar