Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T02:46:14.541Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on connected submetaLindelöf spaces

Published online by Cambridge University Press:  17 April 2009

Nobuyuki Kemoto
Nobuyuki Kemoto
Affiliation:
Department of Mathematics, College of Education, Ryukyu University, Nishihara-Cho, Okinawa, Japan.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we shall show that if m is a natural number and for every 0 ≦ n ≦ m, and 2ω ≦ ωm are assumed, then connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω are Lindelöf. Furthermore, we shall show that 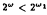if and only if connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω and tightness ≦ ω are Lindelöf.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 40 , Issue 1 , August 1989 , pp. 83 - 89
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Balogh, Z., ‘Paracompactness in locally Lindelöf spaces.’, Caned. J. Math. 38 (1986), 719–727.CrossRefGoogle Scholar
[2]Charlesworth, A., Hodel, R. and Tall, F.D., ‘On a theorem of Jones and Heath concerning discrete subspaces’, Colloq. Math. 34 (1975), 33–37.CrossRefGoogle Scholar
[3]Devlin, K.J., Shelah, S., ‘A weak version of ◊ wnich follows ’, Israel J. Math. 29 (1978), 239–247.CrossRefGoogle Scholar
[4]Engelking, R., Outline of General Topology (Polish Scientific Publishers, Warszawa, 1965).Google Scholar
[5]Jech, T., Set Theory (Academic Press, 1978).Google Scholar
[6]Kunen, K., Set Theory (North-Holland, 1980).Google Scholar
[7]Taylor, A.D., ‘Diamond principles, ideals and the normal Moore problem’, Canad. J. Math. 33 (1981), 282–296.CrossRefGoogle Scholar